LV ellipsoid coupled to a 0D circulatory model and a 0D cell model#
This example demonstrates a multiscale cardiac simulation coupling three distinct models:
3D Mechanics: An idealized Left Ventricle (LV) ellipsoid model solving the balance of linear momentum with active contraction.
0D Circulation: A lumped-parameter model of the closed-loop circulatory system [RSA+22].
0D Electrophysiology: A cellular model for human ventricular myocytes [TBOP+19] coupled with an excitation-contraction model [LPHS+17].
Coupling Strategy#
The coupling is achieved through a segregated approach:
Electrophysiology \(\rightarrow\) Mechanics: The 0D cell model (TorOrd-Land) is pre-solved to generate a time-dependent active tension transient \(T_a(t)\). This \(T_a(t)\) drives the active stress in the 3D mechanics model: \(\mathbf{S}_{active} = T_a(t) \mathbf{f}_0 \otimes \mathbf{f}_0\).
Circulation \(\leftrightarrow\) Mechanics: The 0D circulation model dictates the boundary conditions for the 3D mechanics model, and vice-versa. We use a volume-based coupling strategy:
The circulation model computes the new ventricular volume \(V_{n+1}\) at the next time step.
The 3D mechanics model solves a boundary value problem to find the cavity pressure \(P_{n+1}\) required to achieve this volume \(V_{n+1}\) (given the current activation \(T_a(t_{n+1})\)).
This pressure \(P_{n+1}\) is fed back to the circulation model.
Mathematical Models#
3D Mechanics#
Geometry: Idealized LV ellipsoid with fiber architecture.
Material: Transversely isotropic Holzapfel-Ogden model.
Active Stress: \(\mathbf{S}_{active} = T_a \mathbf{f}_0 \otimes \mathbf{f}_0\).
Boundary Conditions:
Epicardium & Base: Robin BCs (springs) to mimic pericardial constraint and prevent rigid body motion.
Endocardium: The pressure \(P\) is a Lagrange multiplier enforcing the volume constraint \(V(\mathbf{u}) = V_{target}\).
0D Circulation [Regazzoni et al. 2022]#
A closed-loop lumped-parameter network representing the systemic and pulmonary circulation. It includes 4 chambers (LA, LV, RA, RV) and systemic/pulmonary arteries and veins. In this example, we replace the 0D description of the LV with our 3D finite element model.
0D Cell Model [Tomek et al. 2019 + Land et al. 2017]#
TorOrd: Detailed human ventricular action potential model.
Land: Mechanical model describing cross-bridge dynamics and calcium binding to Troponin-C.
from pathlib import Path
from mpi4py import MPI
import dolfinx
import logging
import circulation
import os
import math
from functools import lru_cache
from dolfinx import log
from matplotlib.gridspec import GridSpec
import matplotlib.pyplot as plt
import numpy as np
import gotranx
import adios4dolfinx
import pulse
import cardiac_geometries
import cardiac_geometries.geometry
Next we set up the logging and the MPI communicator
circulation.log.setup_logging(logging.INFO)
comm = MPI.COMM_WORLD
1. Geometry Generation#
We create the idealized LV geometry with appropriate fibers using cardiac_geometries.
geodir = Path("lv_ellipsoid-time-dependent")
if not geodir.exists():
comm.barrier()
cardiac_geometries.mesh.lv_ellipsoid(
outdir=geodir,
create_fibers=True,
fiber_space="Quadrature_6",
r_short_endo=0.025,
r_short_epi=0.035,
r_long_endo=0.09,
r_long_epi=0.097,
psize_ref=0.03,
mu_apex_endo=-math.pi,
mu_base_endo=-math.acos(5 / 17),
mu_apex_epi=-math.pi,
mu_base_epi=-math.acos(5 / 20),
comm=comm,
fiber_angle_epi=-60,
fiber_angle_endo=60,
)
Info : Reading 'lv_ellipsoid-time-dependent/lv_ellipsoid.msh'...
Info : 54 entities
Info : 191 nodes
Info : 990 elements
Info : Done reading 'lv_ellipsoid-time-dependent/lv_ellipsoid.msh'
[12/17/25 16:04:33] INFO INFO:cardiac_geometries.geometry:Reading geometry from lv_ellipsoid-time-dependent geometry.py:323
If the folder already exist, then we just load the geometry
geo = cardiac_geometries.geometry.Geometry.from_folder(
comm=comm,
folder=geodir,
)
INFO INFO:cardiac_geometries.geometry:Reading geometry from lv_ellipsoid-time-dependent geometry.py:323
Next we transform the geometry to a HeartGeometry object
geometry = pulse.HeartGeometry.from_cardiac_geometries(geo, metadata={"quadrature_degree": 6})
2. Constitutive Model#
We use the standard Holzapfel-Ogden model for passive material properties and an Active Stress model driven by a scalar parameter \(T_a\).
material_params = pulse.HolzapfelOgden.transversely_isotropic_parameters()
material = pulse.HolzapfelOgden(f0=geo.f0, s0=geo.s0, **material_params) # type: ignore
We use an active stress approach with 30% transverse active stress (see pulse.active_stress.transversely_active_stress())
Ta = pulse.Variable(dolfinx.fem.Constant(geometry.mesh, dolfinx.default_scalar_type(0.0)), "kPa")
active_model = pulse.ActiveStress(geo.f0, activation=Ta)
a compressible material model
and assembles the CardiacModel
model = pulse.CardiacModel(
material=material,
active=active_model,
compressibility=comp_model,
)
3. Boundary Conditions#
We apply Robin boundary conditions (springs) to the epicardium and base to represent the pericardium and tissue support.
Crucially, for the endocardium, we use a Cavity Volume Constraint. Instead of applying a known pressure (Neumann BC), we enforce the cavity volume to match a target value provided by the circulation model. The Lagrange multiplier associated with this constraint is the cavity pressure.
alpha_epi = pulse.Variable(
dolfinx.fem.Constant(geometry.mesh, dolfinx.default_scalar_type(1e8)), "Pa / m",
)
robin_epi = pulse.RobinBC(value=alpha_epi, marker=geometry.markers["EPI"][0])
alpha_base = pulse.Variable(
dolfinx.fem.Constant(geometry.mesh, dolfinx.default_scalar_type(1e5)), "Pa / m",
)
robin_base = pulse.RobinBC(value=alpha_base, marker=geometry.markers["BASE"][0])
For the pressure we use a Lagrange multiplier method to enforce a given volume. The resulting Lagrange multiplier will be the pressure in the cavity.
To do this we create a Cavity object with a given volume, and specify which marker to use for the boundary condition.
initial_volume = geo.mesh.comm.allreduce(geometry.volume("ENDO"), op=MPI.SUM)
Volume = dolfinx.fem.Constant(geometry.mesh, dolfinx.default_scalar_type(initial_volume))
cavity = pulse.problem.Cavity(marker="ENDO", volume=Volume)
We also specify the parameters for the problem and say that we want the base to move freely and that the units of the mesh is meters
parameters = {"base_bc": pulse.problem.BaseBC.free, "mesh_unit": "m"}
# Next we set up the problem.
outdir = Path("lv_ellipsoid_time_dependent_circulation_static")
bcs = pulse.BoundaryConditions(robin=(robin_epi, robin_base))
problem = pulse.problem.StaticProblem(model=model, geometry=geometry, bcs=bcs, cavities=[cavity], parameters=parameters)
outdir.mkdir(exist_ok=True)
Now we can solve the problem
log.set_log_level(log.LogLevel.INFO)
problem.solve()
[12/17/25 16:04:49] INFO INFO:scifem.solvers:Newton iteration 1: r (abs) = 16.37814370142783 (tol=1e-06), r (rel) = 1.0 (tol=1e-10) solvers.py:279
INFO INFO:scifem.solvers:Newton iteration 2: r (abs) = 2.351332398180868 (tol=1e-06), r (rel) = 0.14356525629799433 (tol=1e-10) solvers.py:279
INFO INFO:scifem.solvers:Newton iteration 3: r (abs) = 0.0030070440603586802 (tol=1e-06), r (rel) = 0.0001836010304450149 (tol=1e-10) solvers.py:279
INFO INFO:scifem.solvers:Newton iteration 4: r (abs) = 1.1086579977257598e-08 (tol=1e-06), r (rel) = 6.769130970740646e-10 (tol=1e-10) solvers.py:279
4
We also use the time step from the problem to set the time step for the 0D cell model
dt = 0.001
times = np.arange(0.0, 1.0, dt)
4. Electrophysiology (0D Cell Model)#
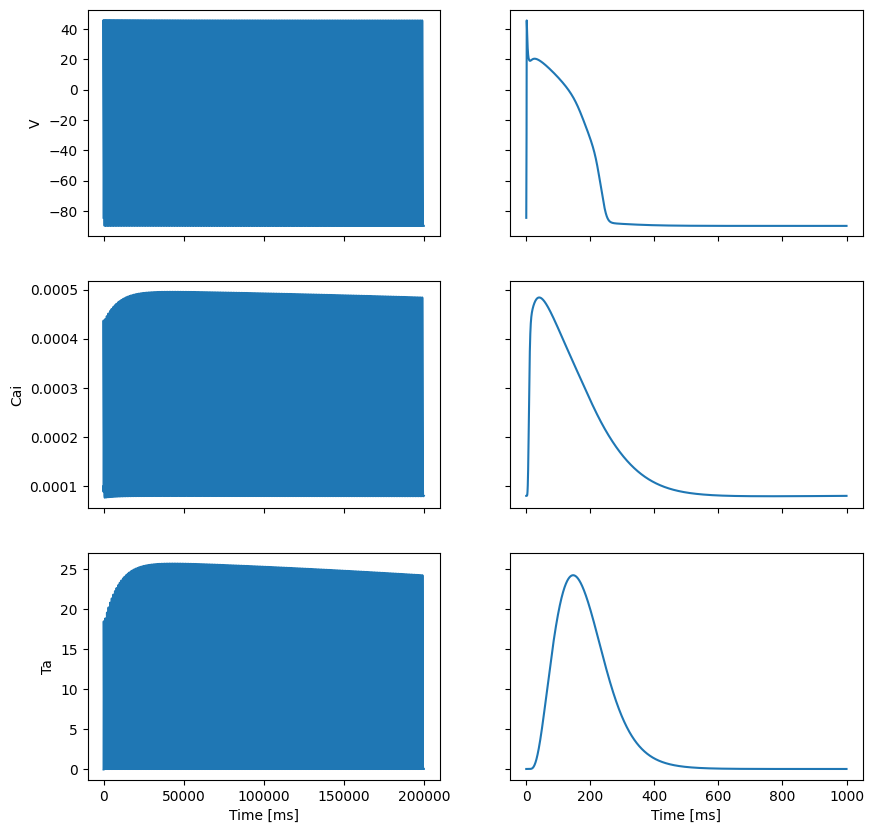
We pre-compute the active tension transient. We load the TorOrd-Land model using gotranx, solve it for 200 beats to reach a limit cycle (steady state), and save the final beat’s active tension trace.
if comm.rank == 0:
ode = gotranx.load_ode("TorOrdLand.ode")
ode = ode.remove_singularities()
code = gotranx.cli.gotran2py.get_code(
ode, scheme=[gotranx.schemes.Scheme.generalized_rush_larsen], shape=gotranx.codegen.base.Shape.single,
)
Path("TorOrdLand.py").write_text(code)
comm.barrier()
import TorOrdLand
2025-12-17 16:04:50 [info ] Load ode TorOrdLand.ode
2025-12-17 16:04:50 [info ] Num states 52
2025-12-17 16:04:50 [info ] Num parameters 140
TorOrdLand_model = TorOrdLand.__dict__
Ta_index = TorOrdLand_model["monitor_index"]("Ta")
y = TorOrdLand_model["init_state_values"]()
# Get initial parameter values
p = TorOrdLand_model["init_parameter_values"]()
import numba
fgr = numba.njit(TorOrdLand_model["generalized_rush_larsen"])
mon = numba.njit(TorOrdLand_model["monitor_values"])
V_index = TorOrdLand_model["state_index"]("v")
Ca_index = TorOrdLand_model["state_index"]("cai")
In the cell model the unit of time is in millisenconds, and we set the time step to 0.1 ms
# Time in milliseconds
dt_cell = 0.1
Now we solve the cell model for 200 beats and save the state at the end of the simulation
state_file = outdir / "state.npy"
if not state_file.is_file():
@numba.jit(nopython=True)
def solve_beat(times, states, dt, p, V_index, Ca_index, Vs, Cais, Tas):
for i, ti in enumerate(times):
states[:] = fgr(states, ti, dt, p)
Vs[i] = states[V_index]
Cais[i] = states[Ca_index]
monitor = mon(ti, states, p)
Tas[i] = monitor[Ta_index]
# Time in milliseconds
nbeats = 200
T = 1000.00
times = np.arange(0, T, dt_cell)
all_times = np.arange(0, T * nbeats, dt_cell)
Vs = np.zeros(len(times) * nbeats)
Cais = np.zeros(len(times) * nbeats)
Tas = np.zeros(len(times) * nbeats)
for beat in range(nbeats):
print(f"Solving beat {beat}")
V_tmp = Vs[beat * len(times) : (beat + 1) * len(times)]
Cai_tmp = Cais[beat * len(times) : (beat + 1) * len(times)]
Ta_tmp = Tas[beat * len(times) : (beat + 1) * len(times)]
solve_beat(times, y, dt_cell, p, V_index, Ca_index, V_tmp, Cai_tmp, Ta_tmp)
fig, ax = plt.subplots(3, 2, sharex="col", sharey="row", figsize=(10, 10))
ax[0, 0].plot(all_times, Vs)
ax[1, 0].plot(all_times, Cais)
ax[2, 0].plot(all_times, Tas)
ax[0, 1].plot(times, Vs[-len(times):])
ax[1, 1].plot(times, Cais[-len(times):])
ax[2, 1].plot(times, Tas[-len(times):])
ax[0, 0].set_ylabel("V")
ax[1, 0].set_ylabel("Cai")
ax[2, 0].set_ylabel("Ta")
ax[2, 0].set_xlabel("Time [ms]")
ax[2, 1].set_xlabel("Time [ms]")
fig.savefig(outdir / "Ta_ORdLand.png")
np.save(state_file, y)
Solving beat 0
Solving beat 1
Solving beat 2
Solving beat 3
Solving beat 4
Solving beat 5
Solving beat 6
Solving beat 7
Solving beat 8
Solving beat 9
Solving beat 10
Solving beat 11
Solving beat 12
Solving beat 13
Solving beat 14
Solving beat 15
Solving beat 16
Solving beat 17
Solving beat 18
Solving beat 19
Solving beat 20
Solving beat 21
Solving beat 22
Solving beat 23
Solving beat 24
Solving beat 25
Solving beat 26
Solving beat 27
Solving beat 28
Solving beat 29
Solving beat 30
Solving beat 31
Solving beat 32
Solving beat 33
Solving beat 34
Solving beat 35
Solving beat 36
Solving beat 37
Solving beat 38
Solving beat 39
Solving beat 40
Solving beat 41
Solving beat 42
Solving beat 43
Solving beat 44
Solving beat 45
Solving beat 46
Solving beat 47
Solving beat 48
Solving beat 49
Solving beat 50
Solving beat 51
Solving beat 52
Solving beat 53
Solving beat 54
Solving beat 55
Solving beat 56
Solving beat 57
Solving beat 58
Solving beat 59
Solving beat 60
Solving beat 61
Solving beat 62
Solving beat 63
Solving beat 64
Solving beat 65
Solving beat 66
Solving beat 67
Solving beat 68
Solving beat 69
Solving beat 70
Solving beat 71
Solving beat 72
Solving beat 73
Solving beat 74
Solving beat 75
Solving beat 76
Solving beat 77
Solving beat 78
Solving beat 79
Solving beat 80
Solving beat 81
Solving beat 82
Solving beat 83
Solving beat 84
Solving beat 85
Solving beat 86
Solving beat 87
Solving beat 88
Solving beat 89
Solving beat 90
Solving beat 91
Solving beat 92
Solving beat 93
Solving beat 94
Solving beat 95
Solving beat 96
Solving beat 97
Solving beat 98
Solving beat 99
Solving beat 100
Solving beat 101
Solving beat 102
Solving beat 103
Solving beat 104
Solving beat 105
Solving beat 106
Solving beat 107
Solving beat 108
Solving beat 109
Solving beat 110
Solving beat 111
Solving beat 112
Solving beat 113
Solving beat 114
Solving beat 115
Solving beat 116
Solving beat 117
Solving beat 118
Solving beat 119
Solving beat 120
Solving beat 121
Solving beat 122
Solving beat 123
Solving beat 124
Solving beat 125
Solving beat 126
Solving beat 127
Solving beat 128
Solving beat 129
Solving beat 130
Solving beat 131
Solving beat 132
Solving beat 133
Solving beat 134
Solving beat 135
Solving beat 136
Solving beat 137
Solving beat 138
Solving beat 139
Solving beat 140
Solving beat 141
Solving beat 142
Solving beat 143
Solving beat 144
Solving beat 145
Solving beat 146
Solving beat 147
Solving beat 148
Solving beat 149
Solving beat 150
Solving beat 151
Solving beat 152
Solving beat 153
Solving beat 154
Solving beat 155
Solving beat 156
Solving beat 157
Solving beat 158
Solving beat 159
Solving beat 160
Solving beat 161
Solving beat 162
Solving beat 163
Solving beat 164
Solving beat 165
Solving beat 166
Solving beat 167
Solving beat 168
Solving beat 169
Solving beat 170
Solving beat 171
Solving beat 172
Solving beat 173
Solving beat 174
Solving beat 175
Solving beat 176
Solving beat 177
Solving beat 178
Solving beat 179
Solving beat 180
Solving beat 181
Solving beat 182
Solving beat 183
Solving beat 184
Solving beat 185
Solving beat 186
Solving beat 187
Solving beat 188
Solving beat 189
Solving beat 190
Solving beat 191
Solving beat 192
Solving beat 193
Solving beat 194
Solving beat 195
Solving beat 196
Solving beat 197
Solving beat 198
Solving beat 199
Next we load the state of the cell model and create an ODEState object. This is a simple wrapper around the cell model that allows us to step the model forward in time and get the active tension at a given time.
y = np.load(state_file)
class ODEState:
def __init__(self, y, dt_cell, p, t=0.0):
self.y = y
self.dt_cell = dt_cell
self.p = p
self.t = t
def forward(self, t):
for t_cell in np.arange(self.t, t, self.dt_cell):
self.y[:] = fgr(self.y, t_cell, self.dt_cell, self.p)
self.t = t
return self.y[:]
def Ta(self, t):
monitor = mon(t, self.y, p)
return monitor[Ta_index]
ode_state = ODEState(y, dt_cell, p)
@lru_cache
def get_activation(t: float):
# Find index modulo 1000
t_cell_next = t * 1000
ode_state.forward(t_cell_next)
return ode_state.Ta(t_cell_next) * 5.0
Next we will save the displacement of the LV to a file
vtx = dolfinx.io.VTXWriter(geometry.mesh.comm, f"{outdir}/displacement.bp", [problem.u], engine="BP4")
vtx.write(0.0)
Here we also use adios4dolfinx to save the displacement over at different time steps. Currently it is not a straight forward way to save functions and to later load them in a time dependent simulation in FEniCSx. However adios4dolfinx allows us to save the function to a file and later load it in a time dependent simulation. We will first need to save the mesh to the same file.
Ta_history = []
# Next we set up the callback function that will be called at each time step. Here we save the displacement of the LV, the pressure volume loop, and the active tension, and we also plot the pressure volume loop at each time step.
def callback(model, i: int, t: float, save=True):
Ta_history.append(get_activation(t))
if save:
adios4dolfinx.write_function(filename, problem.u, time=t, name="displacement")
vtx.write(t)
if comm.rank == 0:
fig = plt.figure(layout="constrained")
gs = GridSpec(3, 2, figure=fig)
ax1 = fig.add_subplot(gs[:, 0])
ax2 = fig.add_subplot(gs[0, 1])
ax3 = fig.add_subplot(gs[1, 1])
ax4 = fig.add_subplot(gs[2, 1])
ax1.plot(model.history["V_LV"][:i+1], model.history["p_LV"][:i+1])
ax1.set_xlabel("V [mL]")
ax1.set_ylabel("p [mmHg]")
ax2.plot(model.history["time"][:i+1], model.history["p_LV"][:i+1])
ax2.set_ylabel("p [mmHg]")
ax3.plot(model.history["time"][:i+1], model.history["V_LV"][:i+1])
ax3.set_ylabel("V [mL]")
ax4.plot(model.history["time"][:i+1], Ta_history[:i+1])
ax4.set_ylabel("Ta [kPa]")
for axi in [ax2, ax3, ax4]:
axi.set_xlabel("Time [s]")
print(f"Saving figure to {outdir / 'pv_loop_incremental.png'}")
fig.savefig(outdir / "pv_loop_incremental.png")
plt.close(fig)
# fig, ax = plt.subplots(4, 1)
# ax[0].plot(model.history["V_LV"][:i+1], model.history["p_LV"][:i+1])
# ax[0].set_xlabel("V [mL]")
# ax[0].set_ylabel("p [mmHg]")
# ax[1].plot(model.history["time"][:i+1], model.history["p_LV"][:i+1])
# ax[2].plot(model.history["time"][:i+1], model.history["V_LV"][:i+1])
# ax[3].plot(model.history["time"][:i+1], Ta_history[:i+1])
# fig.savefig(outdir / "pv_loop_incremental.png")
# plt.close(fig)
5. Coupling Function: 0D \(\rightarrow\) 3D#
This function defines the interface between the circulation loop and the 3D model.
Input: The circulation model provides the target LV Volume (\(V_{LV}\)) and current time \(t\).
Active State: We query the pre-computed active tension \(T_a(t)\) from the cell model.
Solve 3D: We update the
Volumeconstant in theStaticProblemand the activationTa. The solver then finds the displacement field \(\mathbf{u}\) that satisfies the volume constraint.Output: The Lagrange multiplier associated with the volume constraint is the cavity pressure. We return this pressure (converted to mmHg) to the circulation model.
def p_LV_func(V_LV, t):
print("Calculating pressure at time", t)
value = get_activation(t)
print("Time", t, "Activation", value)
Ta.assign(value)
Volume.value = V_LV * 1e-6
problem.solve()
pendo = problem.cavity_pressures[0]
pendo_kPa = pendo.x.array[0] * 1e-3
return circulation.units.kPa_to_mmHg(pendo_kPa)
6. Run Coupled Simulation#
We initialize the Regazzoni circulation model with our custom pressure function p_LV=p_LV_func.
The model is then integrated in time. At each time step, the circulation model computes a target volume, our 3D model computes the corresponding pressure, and the loop advances.
mL = circulation.units.ureg("mL")
add_units = False
surface_area = geometry.surface_area("ENDO")
initial_volume = geo.mesh.comm.allreduce(geometry.volume("ENDO", u=problem.u), op=MPI.SUM) * 1e6
print(f"Initial volume: {initial_volume}")
init_state = {"V_LV": initial_volume * mL}
[2025-12-17 16:05:58.558] [info] Requesting connectivity (2, 0) - (3, 0)
[2025-12-17 16:05:58.558] [info] Requesting connectivity (3, 0) - (2, 0)
[2025-12-17 16:05:58.558] [info] Requesting connectivity (2, 0) - (3, 0)
[2025-12-17 16:05:58.558] [info] Requesting connectivity (3, 0) - (2, 0)
Initial volume: 135.52291212348666
[2025-12-17 16:05:58.560] [info] Requesting connectivity (2, 0) - (3, 0)
[2025-12-17 16:05:58.560] [info] Requesting connectivity (3, 0) - (2, 0)
[2025-12-17 16:05:58.560] [info] Requesting connectivity (2, 0) - (3, 0)
[2025-12-17 16:05:58.560] [info] Requesting connectivity (3, 0) - (2, 0)
circulation_model_3D = circulation.regazzoni2020.Regazzoni2020(
add_units=add_units,
callback=callback,
p_LV=p_LV_func,
verbose=True,
comm=comm,
outdir=outdir,
initial_state=init_state,
)
# Set end time for early stopping if running in CI
end_time = 2 * dt if os.getenv("CI") else None
circulation_model_3D.solve(num_beats=5, initial_state=init_state, dt=dt, T=end_time)
circulation_model_3D.print_info()
[12/17/25 16:05:58] INFO INFO:circulation.base: base.py:134 Circulation model parameters (Regazzoni2020) ┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┓ ┃ Parameter ┃ Value ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┩ │ HR │ 1.25 hertz │ │ chambers.LA.EA │ 0.07 millimeter_Hg / milliliter │ │ chambers.LA.EB │ 0.18 millimeter_Hg / milliliter │ │ chambers.LA.TC │ 0.17 second │ │ chambers.LA.TR │ 0.17 second │ │ chambers.LA.tC │ 0.9 second │ │ chambers.LA.V0 │ 4.0 milliliter │ │ chambers.LV.EA │ 4.482 millimeter_Hg / milliliter │ │ chambers.LV.EB │ 0.17 millimeter_Hg / milliliter │ │ chambers.LV.TC │ 0.25 second │ │ chambers.LV.TR │ 0.4 second │ │ chambers.LV.tC │ 0.1 second │ │ chambers.LV.V0 │ 42.0 milliliter │ │ chambers.RA.EA │ 0.06 millimeter_Hg / milliliter │ │ chambers.RA.EB │ 0.07 millimeter_Hg / milliliter │ │ chambers.RA.TC │ 0.17 second │ │ chambers.RA.TR │ 0.17 second │ │ chambers.RA.tC │ 0.9 second │ │ chambers.RA.V0 │ 4.0 milliliter │ │ chambers.RV.EA │ 0.2 millimeter_Hg / milliliter │ │ chambers.RV.EB │ 0.029 millimeter_Hg / milliliter │ │ chambers.RV.TC │ 0.25 second │ │ chambers.RV.TR │ 0.4 second │ │ chambers.RV.tC │ 0.1 second │ │ chambers.RV.V0 │ 16.0 milliliter │ │ valves.MV.Rmin │ 0.0075 millimeter_Hg * second / milliliter │ │ valves.MV.Rmax │ 75006.2 millimeter_Hg * second / milliliter │ │ valves.AV.Rmin │ 0.0075 millimeter_Hg * second / milliliter │ │ valves.AV.Rmax │ 75006.2 millimeter_Hg * second / milliliter │ │ valves.TV.Rmin │ 0.0075 millimeter_Hg * second / milliliter │ │ valves.TV.Rmax │ 75006.2 millimeter_Hg * second / milliliter │ │ valves.PV.Rmin │ 0.0075 millimeter_Hg * second / milliliter │ │ valves.PV.Rmax │ 75006.2 millimeter_Hg * second / milliliter │ │ circulation.SYS.R_AR │ 0.733 millimeter_Hg * second / milliliter │ │ circulation.SYS.C_AR │ 1.372 milliliter / millimeter_Hg │ │ circulation.SYS.R_VEN │ 0.32 millimeter_Hg * second / milliliter │ │ circulation.SYS.C_VEN │ 11.363 milliliter / millimeter_Hg │ │ circulation.SYS.L_AR │ 0.005 millimeter_Hg * second ** 2 / milliliter │ │ circulation.SYS.L_VEN │ 0.0005 millimeter_Hg * second ** 2 / milliliter │ │ circulation.PUL.R_AR │ 0.046 millimeter_Hg * second / milliliter │ │ circulation.PUL.C_AR │ 20.0 milliliter / millimeter_Hg │ │ circulation.PUL.R_VEN │ 0.0015 millimeter_Hg * second / milliliter │ │ circulation.PUL.C_VEN │ 16.0 milliliter / millimeter_Hg │ │ circulation.PUL.L_AR │ 0.0005 millimeter_Hg * second ** 2 / milliliter │ │ circulation.PUL.L_VEN │ 0.0005 millimeter_Hg * second ** 2 / milliliter │ │ circulation.external.start_withdrawal │ 0.0 second │ │ circulation.external.end_withdrawal │ 0.0 second │ │ circulation.external.start_infusion │ 0.0 second │ │ circulation.external.end_infusion │ 0.0 second │ │ circulation.external.flow_withdrawal │ 0.0 milliliter / second │ │ circulation.external.flow_infusion │ 0.0 milliliter / second │ └───────────────────────────────────────┴─────────────────────────────────────────────────┘
INFO INFO:circulation.base: base.py:141 Circulation model initial states (Regazzoni2020) ┏━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┓ ┃ State ┃ Value ┃ ┡━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┩ │ V_LA │ 80.0 milliliter │ │ V_LV │ 135.52291212348666 milliliter │ │ V_RA │ 80.0 milliliter │ │ V_RV │ 110.0 milliliter │ │ p_AR_SYS │ 70.0 millimeter_Hg │ │ p_VEN_SYS │ 28.32334306787334 millimeter_Hg │ │ p_AR_PUL │ 25.0 millimeter_Hg │ │ p_VEN_PUL │ 20.0 millimeter_Hg │ │ Q_AR_SYS │ 0.0 milliliter / second │ │ Q_VEN_SYS │ 0.0 milliliter / second │ │ Q_AR_PUL │ 0.0 milliliter / second │ │ Q_VEN_PUL │ 0.0 milliliter / second │ └───────────┴─────────────────────────────────┘
Calculating pressure at time 0.0
Time 0.0 Activation 0.2849891894884486
INFO INFO:scifem.solvers:Newton iteration 1: r (abs) = 54.58979988374112 (tol=1e-06), r (rel) = 1.0 (tol=1e-10) solvers.py:279
INFO INFO:scifem.solvers:Newton iteration 2: r (abs) = 0.07053782110752493 (tol=1e-06), r (rel) = 0.0012921428775659193 (tol=1e-10) solvers.py:279
[12/17/25 16:05:59] INFO INFO:scifem.solvers:Newton iteration 3: r (abs) = 0.003950132031159585 (tol=1e-06), r (rel) = 7.236025850199317e-05 (tol=1e-10) solvers.py:279
INFO INFO:scifem.solvers:Newton iteration 4: r (abs) = 3.1664313064583153e-07 (tol=1e-06), r (rel) = 5.800408342221084e-09 (tol=1e-10) solvers.py:279
Calculating pressure at time 0.0
Time 0.0 Activation 0.2849891894884486
INFO INFO:scifem.solvers:Newton iteration 1: r (abs) = 7.162318073860545e-13 (tol=1e-06), r (rel) = 7.162318073860545e-07 (tol=1e-10) solvers.py:279
Saving figure to lv_ellipsoid_time_dependent_circulation_static/pv_loop_incremental.png
INFO INFO:circulation.base: base.py:508 Volumes ┏━━━━━━━━┳━━━━━━━━━┳━━━━━━━━┳━━━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┳━━━━━━━━━┳━━━━━━━━━┳━━━━━━━━━┳━━━━━━━━━━┓ ┃ V_LA ┃ V_LV ┃ V_RA ┃ V_RV ┃ V_AR_SYS ┃ V_VEN_SYS ┃ V_AR_PUL ┃ V_VEN_PUL ┃ Heart ┃ SYS ┃ PUL ┃ Total ┃ ┡━━━━━━━━╇━━━━━━━━━╇━━━━━━━━╇━━━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━╇━━━━━━━━━╇━━━━━━━━━╇━━━━━━━━━╇━━━━━━━━━━┩ │ 78.214 │ 137.309 │ 79.656 │ 110.344 │ 96.040 │ 321.838 │ 500.000 │ 320.000 │ 405.523 │ 417.878 │ 820.000 │ 1643.401 │ └────────┴─────────┴────────┴─────────┴──────────┴───────────┴──────────┴───────────┴─────────┴─────────┴─────────┴──────────┘ Pressures ┏━━━━━━━━┳━━━━━━━┳━━━━━━━┳━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┓ ┃ p_LA ┃ p_LV ┃ p_RA ┃ p_RV ┃ p_AR_SYS ┃ p_VEN_SYS ┃ p_AR_PUL ┃ p_VEN_PUL ┃ ┡━━━━━━━━╇━━━━━━━╇━━━━━━━╇━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━┩ │ 13.680 │ 0.269 │ 5.320 │ 2.726 │ 70.000 │ 28.323 │ 25.000 │ 20.000 │ └────────┴───────┴───────┴───────┴──────────┴───────────┴──────────┴───────────┘ Flows ┏━━━━━━━━━━┳━━━━━━━━┳━━━━━━━━━┳━━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┓ ┃ Q_MV ┃ Q_AV ┃ Q_TV ┃ Q_PV ┃ Q_AR_SYS ┃ Q_VEN_SYS ┃ Q_AR_PUL ┃ Q_VEN_PUL ┃ ┡━━━━━━━━━━╇━━━━━━━━╇━━━━━━━━━╇━━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━┩ │ 1785.897 │ -0.001 │ 343.696 │ -0.000 │ 8.335 │ 46.007 │ 10.000 │ 12.640 │ └──────────┴────────┴─────────┴────────┴──────────┴───────────┴──────────┴───────────┘
Calculating pressure at time 0.001
Time 0.001 Activation 0.28501827278006825
INFO INFO:scifem.solvers:Newton iteration 1: r (abs) = 137.92197235418072 (tol=1e-06), r (rel) = 1.0 (tol=1e-10) solvers.py:279
[12/17/25 16:06:00] INFO INFO:scifem.solvers:Newton iteration 2: r (abs) = 4.4708664322924925 (tol=1e-06), r (rel) = 0.03241591137350763 (tol=1e-10) solvers.py:279
INFO INFO:scifem.solvers:Newton iteration 3: r (abs) = 0.30878346347085894 (tol=1e-06), r (rel) = 0.002238827202078502 (tol=1e-10) solvers.py:279
INFO INFO:scifem.solvers:Newton iteration 4: r (abs) = 0.00037985729639993145 (tol=1e-06), r (rel) = 2.754146347504848e-06 (tol=1e-10) solvers.py:279
INFO INFO:scifem.solvers:Newton iteration 5: r (abs) = 2.0893806814523058e-08 (tol=1e-06), r (rel) = 1.5149005236720514e-10 (tol=1e-10) solvers.py:279
Saving figure to lv_ellipsoid_time_dependent_circulation_static/pv_loop_incremental.png
INFO INFO:circulation.base: base.py:508 Volumes ┏━━━━━━━━┳━━━━━━━━━┳━━━━━━━━┳━━━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┳━━━━━━━━━┳━━━━━━━━━┳━━━━━━━━━┳━━━━━━━━━━┓ ┃ V_LA ┃ V_LV ┃ V_RA ┃ V_RV ┃ V_AR_SYS ┃ V_VEN_SYS ┃ V_AR_PUL ┃ V_VEN_PUL ┃ Heart ┃ SYS ┃ PUL ┃ Total ┃ ┡━━━━━━━━╇━━━━━━━━━╇━━━━━━━━╇━━━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━╇━━━━━━━━━╇━━━━━━━━━╇━━━━━━━━━╇━━━━━━━━━━┩ │ 76.626 │ 138.909 │ 79.363 │ 110.683 │ 96.032 │ 321.800 │ 499.990 │ 319.997 │ 405.582 │ 417.832 │ 819.987 │ 1643.401 │ └────────┴─────────┴────────┴─────────┴──────────┴───────────┴──────────┴───────────┴─────────┴─────────┴─────────┴──────────┘ Pressures ┏━━━━━━━━┳━━━━━━━┳━━━━━━━┳━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┓ ┃ p_LA ┃ p_LV ┃ p_RA ┃ p_RV ┃ p_AR_SYS ┃ p_VEN_SYS ┃ p_AR_PUL ┃ p_VEN_PUL ┃ ┡━━━━━━━━╇━━━━━━━╇━━━━━━━╇━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━┩ │ 13.359 │ 1.340 │ 5.296 │ 2.736 │ 69.994 │ 28.320 │ 24.999 │ 20.000 │ └────────┴───────┴───────┴───────┴──────────┴───────────┴──────────┴───────────┘ Flows ┏━━━━━━━━━━┳━━━━━━━━┳━━━━━━━━━┳━━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┓ ┃ Q_MV ┃ Q_AV ┃ Q_TV ┃ Q_PV ┃ Q_AR_SYS ┃ Q_VEN_SYS ┃ Q_AR_PUL ┃ Q_VEN_PUL ┃ ┡━━━━━━━━━━╇━━━━━━━━╇━━━━━━━━━╇━━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━┩ │ 1600.322 │ -0.001 │ 339.159 │ -0.000 │ 15.449 │ 62.617 │ 19.080 │ 25.885 │ └──────────┴────────┴─────────┴────────┴──────────┴───────────┴──────────┴───────────┘
INFO INFO:circulation.base: base.py:508 Volumes ┏━━━━━━━━┳━━━━━━━━━┳━━━━━━━━┳━━━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┳━━━━━━━━━┳━━━━━━━━━┳━━━━━━━━━┳━━━━━━━━━━┓ ┃ V_LA ┃ V_LV ┃ V_RA ┃ V_RV ┃ V_AR_SYS ┃ V_VEN_SYS ┃ V_AR_PUL ┃ V_VEN_PUL ┃ Heart ┃ SYS ┃ PUL ┃ Total ┃ ┡━━━━━━━━╇━━━━━━━━━╇━━━━━━━━╇━━━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━╇━━━━━━━━━╇━━━━━━━━━╇━━━━━━━━━╇━━━━━━━━━━┩ │ 76.626 │ 138.909 │ 79.363 │ 110.683 │ 96.032 │ 321.800 │ 499.990 │ 319.997 │ 405.582 │ 417.832 │ 819.987 │ 1643.401 │ └────────┴─────────┴────────┴─────────┴──────────┴───────────┴──────────┴───────────┴─────────┴─────────┴─────────┴──────────┘ Pressures ┏━━━━━━━━┳━━━━━━━┳━━━━━━━┳━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┓ ┃ p_LA ┃ p_LV ┃ p_RA ┃ p_RV ┃ p_AR_SYS ┃ p_VEN_SYS ┃ p_AR_PUL ┃ p_VEN_PUL ┃ ┡━━━━━━━━╇━━━━━━━╇━━━━━━━╇━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━┩ │ 13.359 │ 1.340 │ 5.296 │ 2.736 │ 69.994 │ 28.320 │ 24.999 │ 20.000 │ └────────┴───────┴───────┴───────┴──────────┴───────────┴──────────┴───────────┘ Flows ┏━━━━━━━━━━┳━━━━━━━━┳━━━━━━━━━┳━━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┓ ┃ Q_MV ┃ Q_AV ┃ Q_TV ┃ Q_PV ┃ Q_AR_SYS ┃ Q_VEN_SYS ┃ Q_AR_PUL ┃ Q_VEN_PUL ┃ ┡━━━━━━━━━━╇━━━━━━━━╇━━━━━━━━━╇━━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━┩ │ 1600.322 │ -0.001 │ 339.159 │ -0.000 │ 15.449 │ 62.617 │ 19.080 │ 25.885 │ └──────────┴────────┴─────────┴────────┴──────────┴───────────┴──────────┴───────────┘
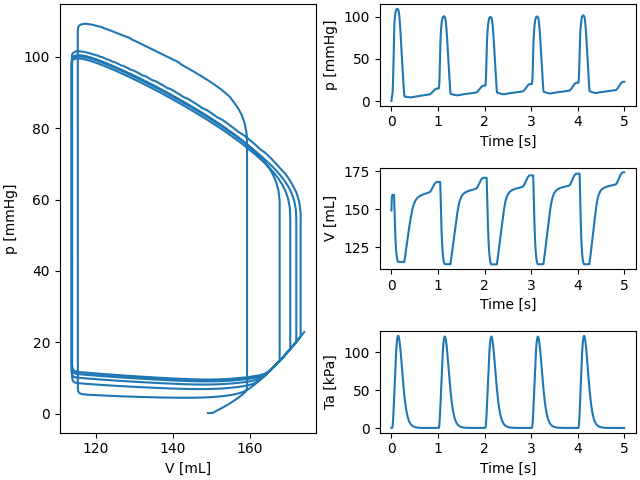
Fig. 1 Pressure volume loop for the LV.#
References#
Sander Land, So-Jin Park-Holohan, Nicolas P Smith, Cristobal G Dos Remedios, Jonathan C Kentish, and Steven A Niederer. A model of cardiac contraction based on novel measurements of tension development in human cardiomyocytes. Journal of molecular and cellular cardiology, 106:68–83, 2017.
Francesco Regazzoni, Matteo Salvador, Pasquale Claudio Africa, Marco Fedele, Luca Dedè, and Alfio Quarteroni. A cardiac electromechanical model coupled with a lumped-parameter model for closed-loop blood circulation. Journal of Computational Physics, 457:111083, 2022.
Jakub Tomek, Alfonso Bueno-Orovio, Elisa Passini, Xin Zhou, Ana Minchole, Oliver Britton, Chiara Bartolucci, Stefano Severi, Alvin Shrier, Laszlo Virag, and others. Development, calibration, and validation of a novel human ventricular myocyte model in health, disease, and drug block. Elife, 8:e48890, 2019.
