Using the command line interface#
The primary usage of gotranx is through the command line interface. For this demonstration we will use a pre-made model that is hosted in the CellML repository. In particular we will be using the original Noble model from 1962 which is probably one of the simplest models for modeling cardiac cells.
First we download the model from the CellML repository by cloning the git repo
git clone https://models.physiomeproject.org/workspace/noble_1962
You could also visit the model page and download the model manually. Once downloaded you will find a file called noble_1962.cellml inside it. Let us see what this file contains
!cat noble_1962.cellml
<?xml version="1.0"?>
<!--
This CellML file was generated on 21/08/2007 at 17:38:21 using:
COR (0.9.31.751)
Copyright 2002-2007 Dr Alan Garny
http://COR.physiol.ox.ac.uk/ - COR@physiol.ox.ac.uk
CellML 1.0 was used to generate this cellular model
http://www.CellML.org/
-->
<model xmlns:dc="http://purl.org/dc/elements/1.1/" xmlns:rdf="http://www.w3.org/1999/02/22-rdf-syntax-ns#" xmlns:bqs="http://www.cellml.org/bqs/1.0#" xmlns:dcterms="http://purl.org/dc/terms/" xmlns:vCard="http://www.w3.org/2001/vcard-rdf/3.0#" xmlns:ns7="http://www.cellml.org/metadata/simulation/1.0#" name="noble_1962" cmeta:id="noble_1962" xmlns="http://www.cellml.org/cellml/1.0#" xmlns:cellml="http://www.cellml.org/cellml/1.0#" xmlns:cmeta="http://www.cellml.org/metadata/1.0#">
<documentation xmlns="http://cellml.org/tmp-documentation">
<article>
<articleinfo>
<title>Noble Purkinje Fibre Model 1962</title>
<author>
<firstname>Catherine</firstname>
<surname>Lloyd</surname>
<affiliation>
<shortaffil>Auckland Bioengineering Institute, The University of Auckland</shortaffil>
</affiliation>
</author>
</articleinfo>
<section id="sec_status">
<title>Model Status</title>
<para>
This CellML model runs in COR, JSim and OpenCell to recreate the published results. The units have been checked and they are consistent.
</para>
</section>
<sect1 id="sec_structure">
<title>Model Structure</title>
<para>
In 1962, Denis Noble published one of the first mathematical models of a cardiac cell. By adapting the equations of the original Hodgkin-Huxley squid axon model (1952), Noble described the long lasting action and pace-maker potentials of the Purkinje fibres of the heart. The potassium-current equations differ from those of Hodgkin and Huxley in that the potassium ions are assumed to flow through two types of channel in the membrane. By contrast, the sodium current equations are very similar to those of Hodgkin and Huxley.
</para>
<para>
The main failure of the Noble (1962) model is that it only includes one voltage gated inward current, I<subscript>Na</subscript>. Calcium currents had not yet been discovered, but there was a clue in the model that something was missing. The only way the model could be made to work was to greatly extend the voltage range of the sodium current by reducing the voltage dependence of the sodium activation process. In effect the sodium current was made to serve the function of both the sodium and the calcium channels as far as the plateau is concerned. There was a clear experimental prediction: either sodium channels in the heart are quantitatively different from those in neurons, or other inward current-carrying channels must exist. Both predictions are correct.
</para>
<para>
The original paper reference is cited below:
</para>
<para>
A Modification of the Hodgkin-Huxley Equations Applicable to Purkinje Fibre Action and Pace-maker Potentials, Noble, D. 1962
<emphasis>Journal of Physiology</emphasis>
, 160, 317-352. <ulink url="http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?cmd=Retrieve&db=PubMed&list_uids=14480151&dopt=Abstract">PubMed ID: 14480151</ulink>
</para>
<informalfigure float="0" id="fig_reaction_diagram">
<mediaobject>
<imageobject>
<objectinfo>
<title>model diagram</title>
</objectinfo>
<imagedata fileref="hodgkin_1952.png"/>
</imageobject>
</mediaobject>
<caption>A schematic cell diagram describing the current flows across the cell membrane that are captured in the Noble 1962 model. Note that this image is identical to the schematic diagram which describes the Hodgkin-Huxley 1952 model. This is because the Noble 1962 model is based on the HH 1952 model, and the ony differences are in the parameters of the model, and also the gating of the potassium channel - and these differences do not show in the schematic diagram.</caption>
</informalfigure>
</sect1>
</article>
</documentation>
<units name="per_second">
<unit exponent="-1" units="second"/>
</units>
<units name="millivolt">
<unit prefix="milli" units="volt"/>
</units>
<units name="per_millivolt">
<unit exponent="-1" prefix="milli" units="volt"/>
</units>
<units name="per_millivolt_second">
<unit exponent="-1" units="millivolt"/>
<unit exponent="-1" units="second"/>
</units>
<units name="microS">
<unit prefix="micro" units="siemens"/>
</units>
<units name="microF">
<unit prefix="micro" units="farad"/>
</units>
<units name="nanoA">
<unit prefix="nano" units="ampere"/>
</units>
<component name="environment">
<variable cmeta:id="environment_time" name="time" public_interface="out" units="second"/>
</component>
<component name="membrane">
<variable cmeta:id="membrane_V" initial_value="-87" name="V" public_interface="out" units="millivolt"/>
<variable initial_value="12" name="Cm" units="microF"/>
<variable name="time" public_interface="in" units="second"/>
<variable name="i_Na" public_interface="in" units="nanoA"/>
<variable name="i_K" public_interface="in" units="nanoA"/>
<variable name="i_Leak" public_interface="in" units="nanoA"/>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<apply>
<eq/>
<apply>
<diff/>
<bvar>
<ci>time</ci>
</bvar>
<ci>V</ci>
</apply>
<apply>
<divide/>
<apply>
<minus/>
<apply>
<plus/>
<ci>i_Na</ci>
<ci>i_K</ci>
<ci>i_Leak</ci>
</apply>
</apply>
<ci>Cm</ci>
</apply>
</apply>
</math>
</component>
<component name="sodium_channel">
<variable cmeta:id="sodium_channel_i_Na" name="i_Na" public_interface="out" units="nanoA"/>
<variable initial_value="400000" name="g_Na_max" units="microS"/>
<variable name="g_Na" units="microS"/>
<variable initial_value="40" name="E_Na" units="millivolt"/>
<variable name="time" private_interface="out" public_interface="in" units="second"/>
<variable name="V" private_interface="out" public_interface="in" units="millivolt"/>
<variable name="m" private_interface="in" units="dimensionless"/>
<variable name="h" private_interface="in" units="dimensionless"/>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<apply>
<eq/>
<ci>g_Na</ci>
<apply>
<times/>
<apply>
<power/>
<ci>m</ci>
<cn xmlns:cellml="http://www.cellml.org/cellml/1.0#" cellml:units="dimensionless">3</cn>
</apply>
<ci>h</ci>
<ci>g_Na_max</ci>
</apply>
</apply>
<apply>
<eq/>
<ci>i_Na</ci>
<apply>
<times/>
<apply>
<plus/>
<ci>g_Na</ci>
<cn xmlns:cellml="http://www.cellml.org/cellml/1.0#" cellml:units="microS">140</cn>
</apply>
<apply>
<minus/>
<ci>V</ci>
<ci>E_Na</ci>
</apply>
</apply>
</apply>
</math>
</component>
<component name="sodium_channel_m_gate">
<variable initial_value="0.01" name="m" public_interface="out" units="dimensionless"/>
<variable name="alpha_m" units="per_second"/>
<variable name="beta_m" units="per_second"/>
<variable name="V" public_interface="in" units="millivolt"/>
<variable name="time" public_interface="in" units="second"/>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<apply>
<eq/>
<ci>alpha_m</ci>
<apply>
<divide/>
<apply>
<times/>
<cn xmlns:cellml="http://www.cellml.org/cellml/1.0#" cellml:units="per_millivolt_second">100</cn>
<apply>
<minus/>
<apply>
<minus/>
<ci>V</ci>
</apply>
<cn xmlns:cellml="http://www.cellml.org/cellml/1.0#" cellml:units="millivolt">48</cn>
</apply>
</apply>
<apply>
<minus/>
<apply>
<exp/>
<apply>
<divide/>
<apply>
<minus/>
<apply>
<minus/>
<ci>V</ci>
</apply>
<cn xmlns:cellml="http://www.cellml.org/cellml/1.0#" cellml:units="millivolt">48</cn>
</apply>
<cn xmlns:cellml="http://www.cellml.org/cellml/1.0#" cellml:units="millivolt">15</cn>
</apply>
</apply>
<cn xmlns:cellml="http://www.cellml.org/cellml/1.0#" cellml:units="dimensionless">1</cn>
</apply>
</apply>
</apply>
<apply>
<eq/>
<ci>beta_m</ci>
<apply>
<divide/>
<apply>
<times/>
<cn xmlns:cellml="http://www.cellml.org/cellml/1.0#" cellml:units="per_millivolt_second">120</cn>
<apply>
<plus/>
<ci>V</ci>
<cn xmlns:cellml="http://www.cellml.org/cellml/1.0#" cellml:units="millivolt">8</cn>
</apply>
</apply>
<apply>
<minus/>
<apply>
<exp/>
<apply>
<divide/>
<apply>
<plus/>
<ci>V</ci>
<cn xmlns:cellml="http://www.cellml.org/cellml/1.0#" cellml:units="millivolt">8</cn>
</apply>
<cn xmlns:cellml="http://www.cellml.org/cellml/1.0#" cellml:units="millivolt">5</cn>
</apply>
</apply>
<cn xmlns:cellml="http://www.cellml.org/cellml/1.0#" cellml:units="dimensionless">1</cn>
</apply>
</apply>
</apply>
<apply>
<eq/>
<apply>
<diff/>
<bvar>
<ci>time</ci>
</bvar>
<ci>m</ci>
</apply>
<apply>
<minus/>
<apply>
<times/>
<ci>alpha_m</ci>
<apply>
<minus/>
<cn xmlns:cellml="http://www.cellml.org/cellml/1.0#" cellml:units="dimensionless">1</cn>
<ci>m</ci>
</apply>
</apply>
<apply>
<times/>
<ci>beta_m</ci>
<ci>m</ci>
</apply>
</apply>
</apply>
</math>
</component>
<component name="sodium_channel_h_gate">
<variable initial_value="0.8" name="h" public_interface="out" units="dimensionless"/>
<variable name="alpha_h" units="per_second"/>
<variable name="beta_h" units="per_second"/>
<variable name="V" public_interface="in" units="millivolt"/>
<variable name="time" public_interface="in" units="second"/>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<apply>
<eq/>
<ci>alpha_h</ci>
<apply>
<times/>
<cn xmlns:cellml="http://www.cellml.org/cellml/1.0#" cellml:units="per_second">170</cn>
<apply>
<exp/>
<apply>
<divide/>
<apply>
<minus/>
<apply>
<minus/>
<ci>V</ci>
</apply>
<cn xmlns:cellml="http://www.cellml.org/cellml/1.0#" cellml:units="millivolt">90</cn>
</apply>
<cn xmlns:cellml="http://www.cellml.org/cellml/1.0#" cellml:units="millivolt">20</cn>
</apply>
</apply>
</apply>
</apply>
<apply>
<eq/>
<ci>beta_h</ci>
<apply>
<divide/>
<cn xmlns:cellml="http://www.cellml.org/cellml/1.0#" cellml:units="per_second">1000</cn>
<apply>
<plus/>
<cn xmlns:cellml="http://www.cellml.org/cellml/1.0#" cellml:units="dimensionless">1</cn>
<apply>
<exp/>
<apply>
<divide/>
<apply>
<minus/>
<apply>
<minus/>
<ci>V</ci>
</apply>
<cn xmlns:cellml="http://www.cellml.org/cellml/1.0#" cellml:units="millivolt">42</cn>
</apply>
<cn xmlns:cellml="http://www.cellml.org/cellml/1.0#" cellml:units="millivolt">10</cn>
</apply>
</apply>
</apply>
</apply>
</apply>
<apply>
<eq/>
<apply>
<diff/>
<bvar>
<ci>time</ci>
</bvar>
<ci>h</ci>
</apply>
<apply>
<minus/>
<apply>
<times/>
<ci>alpha_h</ci>
<apply>
<minus/>
<cn xmlns:cellml="http://www.cellml.org/cellml/1.0#" cellml:units="dimensionless">1</cn>
<ci>h</ci>
</apply>
</apply>
<apply>
<times/>
<ci>beta_h</ci>
<ci>h</ci>
</apply>
</apply>
</apply>
</math>
</component>
<component name="potassium_channel">
<variable cmeta:id="potassium_channel_i_K" name="i_K" public_interface="out" units="nanoA"/>
<variable name="g_K1" units="microS"/>
<variable name="g_K2" units="microS"/>
<variable name="time" private_interface="out" public_interface="in" units="second"/>
<variable name="V" private_interface="out" public_interface="in" units="millivolt"/>
<variable name="n" private_interface="in" units="dimensionless"/>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<apply>
<eq/>
<ci>i_K</ci>
<apply>
<times/>
<apply>
<plus/>
<ci>g_K1</ci>
<ci>g_K2</ci>
</apply>
<apply>
<plus/>
<ci>V</ci>
<cn xmlns:cellml="http://www.cellml.org/cellml/1.0#" cellml:units="millivolt">100</cn>
</apply>
</apply>
</apply>
<apply>
<eq/>
<ci>g_K1</ci>
<apply>
<plus/>
<apply>
<times/>
<cn xmlns:cellml="http://www.cellml.org/cellml/1.0#" cellml:units="microS">1200</cn>
<apply>
<exp/>
<apply>
<divide/>
<apply>
<minus/>
<apply>
<minus/>
<ci>V</ci>
</apply>
<cn xmlns:cellml="http://www.cellml.org/cellml/1.0#" cellml:units="millivolt">90</cn>
</apply>
<cn xmlns:cellml="http://www.cellml.org/cellml/1.0#" cellml:units="millivolt">50</cn>
</apply>
</apply>
</apply>
<apply>
<times/>
<cn xmlns:cellml="http://www.cellml.org/cellml/1.0#" cellml:units="microS">15</cn>
<apply>
<exp/>
<apply>
<divide/>
<apply>
<plus/>
<ci>V</ci>
<cn xmlns:cellml="http://www.cellml.org/cellml/1.0#" cellml:units="millivolt">90</cn>
</apply>
<cn xmlns:cellml="http://www.cellml.org/cellml/1.0#" cellml:units="millivolt">60</cn>
</apply>
</apply>
</apply>
</apply>
</apply>
<apply>
<eq/>
<ci>g_K2</ci>
<apply>
<times/>
<cn xmlns:cellml="http://www.cellml.org/cellml/1.0#" cellml:units="microS">1200</cn>
<apply>
<power/>
<ci>n</ci>
<cn xmlns:cellml="http://www.cellml.org/cellml/1.0#" cellml:units="dimensionless">4</cn>
</apply>
</apply>
</apply>
</math>
</component>
<component name="potassium_channel_n_gate">
<variable initial_value="0.01" name="n" public_interface="out" units="dimensionless"/>
<variable name="alpha_n" units="per_second"/>
<variable name="beta_n" units="per_second"/>
<variable name="V" public_interface="in" units="millivolt"/>
<variable name="time" public_interface="in" units="second"/>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<apply>
<eq/>
<ci>alpha_n</ci>
<apply>
<divide/>
<apply>
<times/>
<cn xmlns:cellml="http://www.cellml.org/cellml/1.0#" cellml:units="per_millivolt_second">0.1</cn>
<apply>
<minus/>
<apply>
<minus/>
<ci>V</ci>
</apply>
<cn xmlns:cellml="http://www.cellml.org/cellml/1.0#" cellml:units="millivolt">50</cn>
</apply>
</apply>
<apply>
<minus/>
<apply>
<exp/>
<apply>
<divide/>
<apply>
<minus/>
<apply>
<minus/>
<ci>V</ci>
</apply>
<cn xmlns:cellml="http://www.cellml.org/cellml/1.0#" cellml:units="millivolt">50</cn>
</apply>
<cn xmlns:cellml="http://www.cellml.org/cellml/1.0#" cellml:units="millivolt">10</cn>
</apply>
</apply>
<cn xmlns:cellml="http://www.cellml.org/cellml/1.0#" cellml:units="dimensionless">1</cn>
</apply>
</apply>
</apply>
<apply>
<eq/>
<ci>beta_n</ci>
<apply>
<times/>
<cn xmlns:cellml="http://www.cellml.org/cellml/1.0#" cellml:units="per_second">2</cn>
<apply>
<exp/>
<apply>
<divide/>
<apply>
<minus/>
<apply>
<minus/>
<ci>V</ci>
</apply>
<cn xmlns:cellml="http://www.cellml.org/cellml/1.0#" cellml:units="millivolt">90</cn>
</apply>
<cn xmlns:cellml="http://www.cellml.org/cellml/1.0#" cellml:units="millivolt">80</cn>
</apply>
</apply>
</apply>
</apply>
<apply>
<eq/>
<apply>
<diff/>
<bvar>
<ci>time</ci>
</bvar>
<ci>n</ci>
</apply>
<apply>
<minus/>
<apply>
<times/>
<ci>alpha_n</ci>
<apply>
<minus/>
<cn xmlns:cellml="http://www.cellml.org/cellml/1.0#" cellml:units="dimensionless">1</cn>
<ci>n</ci>
</apply>
</apply>
<apply>
<times/>
<ci>beta_n</ci>
<ci>n</ci>
</apply>
</apply>
</apply>
</math>
</component>
<component name="leakage_current">
<variable cmeta:id="leakage_current_i_Leak" name="i_Leak" public_interface="out" units="nanoA"/>
<variable initial_value="75" name="g_L" units="microS"/>
<variable initial_value="-60" name="E_L" units="millivolt"/>
<variable name="time" public_interface="in" units="second"/>
<variable name="V" public_interface="in" units="millivolt"/>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<apply>
<eq/>
<ci>i_Leak</ci>
<apply>
<times/>
<ci>g_L</ci>
<apply>
<minus/>
<ci>V</ci>
<ci>E_L</ci>
</apply>
</apply>
</apply>
</math>
</component>
<group>
<relationship_ref relationship="containment"/>
<component_ref component="membrane">
<component_ref component="sodium_channel">
<component_ref component="sodium_channel_m_gate"/>
<component_ref component="sodium_channel_h_gate"/>
</component_ref>
<component_ref component="potassium_channel">
<component_ref component="potassium_channel_n_gate"/>
</component_ref>
<component_ref component="leakage_current"/>
</component_ref>
</group>
<group>
<relationship_ref relationship="encapsulation"/>
<component_ref component="sodium_channel">
<component_ref component="sodium_channel_m_gate"/>
<component_ref component="sodium_channel_h_gate"/>
</component_ref>
<component_ref component="potassium_channel">
<component_ref component="potassium_channel_n_gate"/>
</component_ref>
</group>
<connection>
<map_components component_1="membrane" component_2="environment"/>
<map_variables variable_1="time" variable_2="time"/>
</connection>
<connection>
<map_components component_1="sodium_channel" component_2="environment"/>
<map_variables variable_1="time" variable_2="time"/>
</connection>
<connection>
<map_components component_1="potassium_channel" component_2="environment"/>
<map_variables variable_1="time" variable_2="time"/>
</connection>
<connection>
<map_components component_1="leakage_current" component_2="environment"/>
<map_variables variable_1="time" variable_2="time"/>
</connection>
<connection>
<map_components component_1="membrane" component_2="sodium_channel"/>
<map_variables variable_1="V" variable_2="V"/>
<map_variables variable_1="i_Na" variable_2="i_Na"/>
</connection>
<connection>
<map_components component_1="membrane" component_2="potassium_channel"/>
<map_variables variable_1="V" variable_2="V"/>
<map_variables variable_1="i_K" variable_2="i_K"/>
</connection>
<connection>
<map_components component_1="membrane" component_2="leakage_current"/>
<map_variables variable_1="V" variable_2="V"/>
<map_variables variable_1="i_Leak" variable_2="i_Leak"/>
</connection>
<connection>
<map_components component_1="sodium_channel" component_2="sodium_channel_m_gate"/>
<map_variables variable_1="m" variable_2="m"/>
<map_variables variable_1="time" variable_2="time"/>
<map_variables variable_1="V" variable_2="V"/>
</connection>
<connection>
<map_components component_1="sodium_channel" component_2="sodium_channel_h_gate"/>
<map_variables variable_1="h" variable_2="h"/>
<map_variables variable_1="time" variable_2="time"/>
<map_variables variable_1="V" variable_2="V"/>
</connection>
<connection>
<map_components component_1="potassium_channel" component_2="potassium_channel_n_gate"/>
<map_variables variable_1="n" variable_2="n"/>
<map_variables variable_1="time" variable_2="time"/>
<map_variables variable_1="V" variable_2="V"/>
</connection>
<rdf:RDF xmlns:rdf="http://www.w3.org/1999/02/22-rdf-syntax-ns#">
<rdf:Seq rdf:about="rdf:#bde132e3-049c-4da1-8e0a-b4d71b59075d">
<rdf:li rdf:resource="rdf:#da0ccc23-6611-4043-a2fa-3c4c3c5cd673"/>
</rdf:Seq>
<rdf:Description rdf:about="rdf:#93453950-5f08-4363-90bd-aff472ce905e">
<vCard:Given xmlns:vCard="http://www.w3.org/2001/vcard-rdf/3.0#">Peter</vCard:Given>
<vCard:Family xmlns:vCard="http://www.w3.org/2001/vcard-rdf/3.0#">Villiger</vCard:Family>
<vCard:Other xmlns:vCard="http://www.w3.org/2001/vcard-rdf/3.0#">J</vCard:Other>
</rdf:Description>
<rdf:Description rdf:about="rdf:#a97bf273-bccc-41f4-854c-7ae43ce5cc63">
<vCard:Given xmlns:vCard="http://www.w3.org/2001/vcard-rdf/3.0#">Catherine</vCard:Given>
<vCard:Family xmlns:vCard="http://www.w3.org/2001/vcard-rdf/3.0#">Lloyd</vCard:Family>
<vCard:Other xmlns:vCard="http://www.w3.org/2001/vcard-rdf/3.0#">May</vCard:Other>
</rdf:Description>
<rdf:Description rdf:about="">
<dc:publisher xmlns:dc="http://purl.org/dc/elements/1.1/">Auckland Bioengineering Institute</dc:publisher>
<cmeta:comment rdf:resource="rdf:#d2b6f58e-6293-4b50-b751-a6fd3ab1f989"/>
<dcterms:created xmlns:dcterms="http://purl.org/dc/terms/" rdf:resource="rdf:#b8e6ba3c-0914-43bf-8037-1424182388cb"/>
<dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/" rdf:resource="rdf:#6732b89c-f3f7-4b52-b220-223c5e7e6745"/>
<cmeta:modification rdf:resource="rdf:#3fb6dd2b-a5d0-45a9-9b46-ba6b7c47bad6"/>
</rdf:Description>
<rdf:Description rdf:about="rdf:#e5a5bd71-3824-4f00-a109-83d494a47634">
<vCard:FN xmlns:vCard="http://www.w3.org/2001/vcard-rdf/3.0#">Catherine Lloyd</vCard:FN>
</rdf:Description>
<rdf:Description rdf:about="rdf:#7899ef23-ac75-4102-9531-f07bf2391e36">
<rdf:type rdf:resource="http://imc.org/vCard/3.0#internet"/>
<rdf:value>c.lloyd@auckland.ac.nz</rdf:value>
</rdf:Description>
<rdf:Description rdf:about="rdf:#29ec82ff-8775-4a8a-affa-2d23d612180b">
<dcterms:W3CDTF xmlns:dcterms="http://purl.org/dc/terms/">2006-03-31</dcterms:W3CDTF>
</rdf:Description>
<rdf:Description rdf:about="rdf:#4d541118-ca7a-413a-9452-aa240967c7f1">
<vCard:N xmlns:vCard="http://www.w3.org/2001/vcard-rdf/3.0#" rdf:resource="rdf:#17575034-c342-4933-bab3-b4bb597edd4f"/>
</rdf:Description>
<rdf:Description rdf:about="rdf:#e56a5760-9087-425d-add3-5226ae63d572">
<dc:title xmlns:dc="http://purl.org/dc/elements/1.1/">Journal of Physiology</dc:title>
</rdf:Description>
<rdf:Description rdf:about="rdf:#6732b89c-f3f7-4b52-b220-223c5e7e6745">
<vCard:ORG xmlns:vCard="http://www.w3.org/2001/vcard-rdf/3.0#" rdf:resource="rdf:#d8ced495-18cf-42f1-94f0-b660e798b273"/>
<vCard:EMAIL xmlns:vCard="http://www.w3.org/2001/vcard-rdf/3.0#" rdf:resource="rdf:#7899ef23-ac75-4102-9531-f07bf2391e36"/>
<vCard:N xmlns:vCard="http://www.w3.org/2001/vcard-rdf/3.0#" rdf:resource="rdf:#a97bf273-bccc-41f4-854c-7ae43ce5cc63"/>
</rdf:Description>
<rdf:Description rdf:about="rdf:#1ac643bb-53ff-4666-89b0-819cdf84034c">
<vCard:N xmlns:vCard="http://www.w3.org/2001/vcard-rdf/3.0#" rdf:resource="rdf:#93453950-5f08-4363-90bd-aff472ce905e"/>
</rdf:Description>
<rdf:Description rdf:about="rdf:#3fb6dd2b-a5d0-45a9-9b46-ba6b7c47bad6">
<dcterms:modified xmlns:dcterms="http://purl.org/dc/terms/" rdf:resource="rdf:#006c1b33-1b41-4dd2-8bd9-56bc28c91701"/>
<rdf:value>This models has been curated using the unit checker in COR and is now unit-consistent.</rdf:value>
<cmeta:modifier rdf:resource="rdf:#4d541118-ca7a-413a-9452-aa240967c7f1"/>
</rdf:Description>
<rdf:Description rdf:about="rdf:#da0ccc23-6611-4043-a2fa-3c4c3c5cd673">
<rdf:type rdf:resource="http://www.cellml.org/bqs/1.0#Person"/>
<vCard:N xmlns:vCard="http://www.w3.org/2001/vcard-rdf/3.0#" rdf:resource="rdf:#668ac89a-7e3f-4741-b844-d9fccc1d635d"/>
</rdf:Description>
<rdf:Description rdf:about="rdf:#967adaad-713c-4689-a962-e69b626e2248">
<vCard:ORG xmlns:vCard="http://www.w3.org/2001/vcard-rdf/3.0#" rdf:resource="rdf:#e91df542-a47c-43d9-b0ff-b0767719d581"/>
<vCard:EMAIL xmlns:vCard="http://www.w3.org/2001/vcard-rdf/3.0#" rdf:resource="rdf:#1167aea9-f639-491b-90fd-f4b23332d66d"/>
<vCard:N xmlns:vCard="http://www.w3.org/2001/vcard-rdf/3.0#" rdf:resource="rdf:#5a885652-b58c-469d-b4d3-8b4923e85adb"/>
</rdf:Description>
<rdf:Description rdf:about="rdf:#bab8bf9e-26fc-484f-a5b4-2c4a97a1d123">
<dcterms:W3CDTF xmlns:dcterms="http://purl.org/dc/terms/">1962-01-01</dcterms:W3CDTF>
</rdf:Description>
<rdf:Description rdf:about="rdf:#d8ced495-18cf-42f1-94f0-b660e798b273">
<vCard:Orgname xmlns:vCard="http://www.w3.org/2001/vcard-rdf/3.0#">The University of Auckland</vCard:Orgname>
<vCard:Orgunit xmlns:vCard="http://www.w3.org/2001/vcard-rdf/3.0#">Auckland Bioengineering Institute</vCard:Orgunit>
</rdf:Description>
<rdf:Description rdf:about="rdf:#aea6598d-b850-4aa6-9bb7-76452adba692">
<bqs:Pubmed_id xmlns:bqs="http://www.cellml.org/bqs/1.0#">14480151</bqs:Pubmed_id>
<bqs:JournalArticle xmlns:bqs="http://www.cellml.org/bqs/1.0#" rdf:resource="rdf:#9e8fe311-1b9c-477b-a358-d83c2537bbf3"/>
</rdf:Description>
<rdf:Description rdf:about="">
<cmeta:modification rdf:resource="rdf:#fa6607cc-772f-491c-b0bd-c8c641feed13"/>
<dcterms:created xmlns:dcterms="http://purl.org/dc/terms/" rdf:resource="rdf:#4851a981-8fa2-4fc8-a679-cbdb4a1da137"/>
<dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/" rdf:resource="rdf:#967adaad-713c-4689-a962-e69b626e2248"/>
</rdf:Description>
<rdf:Description rdf:about="rdf:#b8e6ba3c-0914-43bf-8037-1424182388cb">
<dcterms:W3CDTF xmlns:dcterms="http://purl.org/dc/terms/">2007-09-07T00:00:00+00:00</dcterms:W3CDTF>
</rdf:Description>
<rdf:Description rdf:about="rdf:#9faaf430-3656-4f95-be79-a1e31be11187">
<vCard:FN xmlns:vCard="http://www.w3.org/2001/vcard-rdf/3.0#">James Lawson</vCard:FN>
</rdf:Description>
<rdf:Description rdf:about="rdf:#9e8fe311-1b9c-477b-a358-d83c2537bbf3">
<dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/" rdf:resource="rdf:#bde132e3-049c-4da1-8e0a-b4d71b59075d"/>
<dc:title xmlns:dc="http://purl.org/dc/elements/1.1/">A Modification of the Hodgkin-Huxley Equations Applicable to Purkinje Fibre Action and Pace-Maker Potentials</dc:title>
<bqs:volume xmlns:bqs="http://www.cellml.org/bqs/1.0#">160</bqs:volume>
<bqs:first_page xmlns:bqs="http://www.cellml.org/bqs/1.0#">317</bqs:first_page>
<bqs:Journal xmlns:bqs="http://www.cellml.org/bqs/1.0#" rdf:resource="rdf:#e56a5760-9087-425d-add3-5226ae63d572"/>
<dcterms:issued xmlns:dcterms="http://purl.org/dc/terms/" rdf:resource="rdf:#bab8bf9e-26fc-484f-a5b4-2c4a97a1d123"/>
<bqs:last_page xmlns:bqs="http://www.cellml.org/bqs/1.0#">352</bqs:last_page>
</rdf:Description>
<rdf:Description rdf:about="rdf:#fa6607cc-772f-491c-b0bd-c8c641feed13">
<dcterms:modified xmlns:dcterms="http://purl.org/dc/terms/" rdf:resource="rdf:#29ec82ff-8775-4a8a-affa-2d23d612180b"/>
<rdf:value>
added metadata
</rdf:value>
<cmeta:modifier rdf:resource="rdf:#1ac643bb-53ff-4666-89b0-819cdf84034c"/>
</rdf:Description>
<rdf:Description rdf:about="rdf:#4851a981-8fa2-4fc8-a679-cbdb4a1da137">
<dcterms:W3CDTF xmlns:dcterms="http://purl.org/dc/terms/">2005-05-04</dcterms:W3CDTF>
</rdf:Description>
<rdf:Description rdf:about="rdf:#017e298c-f99c-41cf-8439-d6a0723656eb">
<dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/" rdf:resource="rdf:#e5a5bd71-3824-4f00-a109-83d494a47634"/>
<rdf:value>This is the CellML description of Noble's 1962 mathematical model of Purkinje fibre action and pace-maker potentials. The equations formulated by Hodgkin and Huxley (1952) to describe the electrical activity of squid nerve have been modified to describe the action and pace-maker potentials of the Purkinje fibres of the heart.</rdf:value>
</rdf:Description>
<rdf:Description rdf:about="#noble_1962">
<bqs:reference xmlns:bqs="http://www.cellml.org/bqs/1.0#" rdf:resource="rdf:#aea6598d-b850-4aa6-9bb7-76452adba692"/>
<bqs:reference xmlns:bqs="http://www.cellml.org/bqs/1.0#" rdf:parseType="Resource">
<dc:subject xmlns:dc="http://purl.org/dc/elements/1.1/" rdf:parseType="Resource">
<bqs:subject_type>keyword</bqs:subject_type>
<rdf:value>
<rdf:Bag>
<rdf:li>purkinje</rdf:li>
<rdf:li>Purkinje fibre</rdf:li>
<rdf:li>electrophysiology</rdf:li>
<rdf:li>pacemaker</rdf:li>
<rdf:li>cardiac</rdf:li>
<rdf:li>Hodgkin-Huxley</rdf:li>
</rdf:Bag>
</rdf:value>
</dc:subject>
</bqs:reference>
<cmeta:comment rdf:resource="rdf:#017e298c-f99c-41cf-8439-d6a0723656eb"/>
</rdf:Description>
<rdf:Description rdf:about="rdf:#1167aea9-f639-491b-90fd-f4b23332d66d">
<rdf:type rdf:resource="http://imc.org/vCard/3.0#internet"/>
<rdf:value>penny.noble@physiol.ox.ac.uk</rdf:value>
</rdf:Description>
<rdf:Description rdf:about="rdf:#d2b6f58e-6293-4b50-b751-a6fd3ab1f989">
<dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/" rdf:resource="rdf:#9faaf430-3656-4f95-be79-a1e31be11187"/>
<rdf:value>This model has been curated by both Penny Noble and James Lawson and is known to run in COR and PCEnv 0.2.</rdf:value>
</rdf:Description>
<rdf:Description rdf:about="rdf:#17575034-c342-4933-bab3-b4bb597edd4f">
<vCard:Given xmlns:vCard="http://www.w3.org/2001/vcard-rdf/3.0#">Penny</vCard:Given>
<vCard:Family xmlns:vCard="http://www.w3.org/2001/vcard-rdf/3.0#">Noble</vCard:Family>
</rdf:Description>
<rdf:Description rdf:about="rdf:#006c1b33-1b41-4dd2-8bd9-56bc28c91701">
<dcterms:W3CDTF xmlns:dcterms="http://purl.org/dc/terms/">2007-09-07T13:50:26+12:00</dcterms:W3CDTF>
</rdf:Description>
<rdf:Description rdf:about="rdf:#668ac89a-7e3f-4741-b844-d9fccc1d635d">
<vCard:Given xmlns:vCard="http://www.w3.org/2001/vcard-rdf/3.0#">D</vCard:Given>
<vCard:Family xmlns:vCard="http://www.w3.org/2001/vcard-rdf/3.0#">Noble</vCard:Family>
</rdf:Description>
<rdf:Description rdf:about="rdf:#5a885652-b58c-469d-b4d3-8b4923e85adb">
<vCard:Given xmlns:vCard="http://www.w3.org/2001/vcard-rdf/3.0#">Penny</vCard:Given>
<vCard:Family xmlns:vCard="http://www.w3.org/2001/vcard-rdf/3.0#">Noble</vCard:Family>
</rdf:Description>
<rdf:Description rdf:about="rdf:#e91df542-a47c-43d9-b0ff-b0767719d581">
<vCard:Orgname xmlns:vCard="http://www.w3.org/2001/vcard-rdf/3.0#">Oxford University</vCard:Orgname>
</rdf:Description>
</rdf:RDF>
</model>
The cellml format is a format similar to XML.
Converting from .cellml to .ode#
We will now convert the .cellml file to a .ode file using the following command
!python3 -m gotranx cellml2ode noble_1962.cellml
2026-03-04 06:22:25 [info ] Converting /home/runner/work/gotranx/gotranx/docs/noble_1962.cellml to gotran ode file
2026-03-04 06:22:25 [info ] Wrote /home/runner/work/gotranx/gotranx/docs/noble_1962.ode
2026-03-04 06:22:25 [info ] Wrote /home/runner/work/gotranx/gotranx/docs/noble_1962.ode
This cellml converter is actually based on a different project called myokit. gotranx allows for converting to and from myokit models and myokit allows for conversion to and from cellml.
Once the conversion is done, we see that a new file called noble_1962.ode has been created with the following content
!cat noble_1962.ode
states("membrane",
V=ScalarParam(-87, unit="mV", description="")
)
states("sodium_channel_h_gate",
h=ScalarParam(0.8, unit="1", description="")
)
states("sodium_channel_m_gate",
m=ScalarParam(0.01, unit="1", description="")
)
states("potassium_channel_n_gate",
n=ScalarParam(0.01, unit="1", description="")
)
parameters("membrane",
Cm=ScalarParam(12.0, unit="uF", description="")
)
parameters("leakage_current",
E_L=ScalarParam(-60.0, unit="mV", description=""),
g_L=ScalarParam(75.0, unit="uS", description="")
)
parameters("sodium_channel",
E_Na=ScalarParam(40.0, unit="mV", description=""),
g_Na_max=ScalarParam(400000.0, unit="uS", description="")
)
expressions("sodium_channel_h_gate")
alpha_h = 170.0*exp((-V - 1*90.0)/20.0) # S/F
beta_h = 1000.0/(exp((-V - 1*42.0)/10.0) + 1.0) # S/F
dh_dt = alpha_h*(1.0 - h) - beta_h*h
expressions("sodium_channel_m_gate")
alpha_m = (100.0*(-V - 1*48.0))/(exp((-V - 1*48.0)/15.0) - 1*1.0) # S/F
beta_m = (120.0*(V + 8.0))/(exp((V + 8.0)/5.0) - 1*1.0) # S/F
dm_dt = alpha_m*(1.0 - m) - beta_m*m
expressions("potassium_channel_n_gate")
alpha_n = (0.1*(-V - 1*50.0))/(exp((-V - 1*50.0)/10.0) - 1*1.0) # S/F
beta_n = 2.0*exp((-V - 1*90.0)/80.0) # S/F
dn_dt = alpha_n*(1.0 - n) - beta_n*n
expressions("potassium_channel")
g_K1 = 1200.0*exp((-V - 1*90.0)/50.0) + 15.0*exp((V + 90.0)/60.0) # uS
g_K2 = 1200.0*n**4.0 # uS
i_K = (V + 100.0)*(g_K1 + g_K2) # nA
expressions("sodium_channel")
g_Na = g_Na_max*(h*m**3.0) # uS
i_Na = (-E_Na + V)*(g_Na + 140.0) # nA
expressions("leakage_current")
i_Leak = g_L*(-E_L + V) # nA
expressions("membrane")
dV_dt = (-(i_Leak + (i_K + i_Na)))/Cm # mV
This file contains the ODE representation that is used by gotranx. Note that you could also just write your own .ode file. Take a look at the grammar to learn more about the DSL.
Generating source code#
Now that we have a .ode file we can use this to generate source code in python (or C) that can be used to solve the ODE. To do this we can use the commands
python3 -m gotranx ode2py noble_1962.ode
Either to at .c file
python3 -m gotranx ode2c noble_1962.ode --to .c
or to a .h file
python3 -m gotranx ode2c noble_1962.ode --to .h
Let us generate some code in python
!python3 -m gotranx ode2py noble_1962.ode
2026-03-04 06:22:26 [info ] Load ode /home/runner/work/gotranx/gotranx/docs/noble_1962.ode
2026-03-04 06:22:26 [info ] Num states 4
2026-03-04 06:22:26 [info ] Num parameters 5
2026-03-04 06:22:26 [info ] Wrote /home/runner/work/gotranx/gotranx/docs/noble_1962.py
Now let us take a look at the generated code
!cat noble_1962.py
import numpy
parameter = {"Cm": 0, "E_L": 1, "E_Na": 2, "g_L": 3, "g_Na_max": 4}
def parameter_index(name: str) -> int:
"""Return the index of the parameter with the given name
Arguments
---------
name : str
The name of the parameter
Returns
-------
int
The index of the parameter
Raises
------
KeyError
If the name is not a valid parameter
"""
return parameter[name]
state = {"h": 0, "m": 1, "n": 2, "V": 3}
def state_index(name: str) -> int:
"""Return the index of the state with the given name
Arguments
---------
name : str
The name of the state
Returns
-------
int
The index of the state
Raises
------
KeyError
If the name is not a valid state
"""
return state[name]
monitor = {
"alpha_h": 0,
"alpha_m": 1,
"alpha_n": 2,
"beta_h": 3,
"beta_m": 4,
"beta_n": 5,
"g_K1": 6,
"g_K2": 7,
"g_Na": 8,
"i_Leak": 9,
"dh_dt": 10,
"dm_dt": 11,
"dn_dt": 12,
"i_K": 13,
"i_Na": 14,
"dV_dt": 15,
}
def monitor_index(name: str) -> int:
"""Return the index of the monitor with the given name
Arguments
---------
name : str
The name of the monitor
Returns
-------
int
The index of the monitor
Raises
------
KeyError
If the name is not a valid monitor
"""
return monitor[name]
def init_parameter_values(**values):
"""Initialize parameter values"""
# Cm=12.0, E_L=-60.0, E_Na=40.0, g_L=75.0, g_Na_max=400000.0
parameters = numpy.array([12.0, -60.0, 40.0, 75.0, 400000.0], dtype=numpy.float64)
for key, value in values.items():
parameters[parameter_index(key)] = value
return parameters
def init_state_values(**values):
"""Initialize state values"""
# h=0.8, m=0.01, n=0.01, V=-87
states = numpy.array([0.8, 0.01, 0.01, -87], dtype=numpy.float64)
for key, value in values.items():
states[state_index(key)] = value
return states
def rhs(t, states, parameters):
# Assign states
h = states[0]
m = states[1]
n = states[2]
V = states[3]
# Assign parameters
Cm = parameters[0]
E_L = parameters[1]
E_Na = parameters[2]
g_L = parameters[3]
g_Na_max = parameters[4]
# Assign expressions
values = numpy.zeros_like(states, dtype=numpy.float64)
alpha_h = 170.0 * numpy.exp((-V - 1 * 90.0) / 20.0)
alpha_m = (100.0 * (-V - 1 * 48.0)) / (numpy.exp((-V - 1 * 48.0) / 15.0) - 1 * 1.0)
alpha_n = (0.1 * (-V - 1 * 50.0)) / (numpy.exp((-V - 1 * 50.0) / 10.0) - 1 * 1.0)
beta_h = 1000.0 / (numpy.exp((-V - 1 * 42.0) / 10.0) + 1.0)
beta_m = (120.0 * (V + 8.0)) / (numpy.exp((V + 8.0) / 5.0) - 1 * 1.0)
beta_n = 2.0 * numpy.exp((-V - 1 * 90.0) / 80.0)
g_K1 = 1200.0 * numpy.exp((-V - 1 * 90.0) / 50.0) + 15.0 * numpy.exp(
(V + 90.0) / 60.0
)
g_K2 = 1200.0 * n**4.0
g_Na = g_Na_max * (h * m**3.0)
i_Leak = g_L * (-E_L + V)
dh_dt = alpha_h * (1.0 - h) - beta_h * h
values[0] = dh_dt
dm_dt = alpha_m * (1.0 - m) - beta_m * m
values[1] = dm_dt
dn_dt = alpha_n * (1.0 - n) - beta_n * n
values[2] = dn_dt
i_K = (V + 100.0) * (g_K1 + g_K2)
i_Na = (-E_Na + V) * (g_Na + 140.0)
dV_dt = (-(i_Leak + (i_K + i_Na))) / Cm
values[3] = dV_dt
return values
def monitor_values(t, states, parameters):
# Assign states
h = states[0]
m = states[1]
n = states[2]
V = states[3]
# Assign parameters
Cm = parameters[0]
E_L = parameters[1]
E_Na = parameters[2]
g_L = parameters[3]
g_Na_max = parameters[4]
# Assign expressions
shape = 16 if len(states.shape) == 1 else (16, states.shape[1])
values = numpy.zeros(shape)
alpha_h = 170.0 * numpy.exp((-V - 1 * 90.0) / 20.0)
values[0] = alpha_h
alpha_m = (100.0 * (-V - 1 * 48.0)) / (numpy.exp((-V - 1 * 48.0) / 15.0) - 1 * 1.0)
values[1] = alpha_m
alpha_n = (0.1 * (-V - 1 * 50.0)) / (numpy.exp((-V - 1 * 50.0) / 10.0) - 1 * 1.0)
values[2] = alpha_n
beta_h = 1000.0 / (numpy.exp((-V - 1 * 42.0) / 10.0) + 1.0)
values[3] = beta_h
beta_m = (120.0 * (V + 8.0)) / (numpy.exp((V + 8.0) / 5.0) - 1 * 1.0)
values[4] = beta_m
beta_n = 2.0 * numpy.exp((-V - 1 * 90.0) / 80.0)
values[5] = beta_n
g_K1 = 1200.0 * numpy.exp((-V - 1 * 90.0) / 50.0) + 15.0 * numpy.exp(
(V + 90.0) / 60.0
)
values[6] = g_K1
g_K2 = 1200.0 * n**4.0
values[7] = g_K2
g_Na = g_Na_max * (h * m**3.0)
values[8] = g_Na
i_Leak = g_L * (-E_L + V)
values[9] = i_Leak
dh_dt = alpha_h * (1.0 - h) - beta_h * h
values[10] = dh_dt
dm_dt = alpha_m * (1.0 - m) - beta_m * m
values[11] = dm_dt
dn_dt = alpha_n * (1.0 - n) - beta_n * n
values[12] = dn_dt
i_K = (V + 100.0) * (g_K1 + g_K2)
values[13] = i_K
i_Na = (-E_Na + V) * (g_Na + 140.0)
values[14] = i_Na
dV_dt = (-(i_Leak + (i_K + i_Na))) / Cm
values[15] = dV_dt
return values
We wee the the code contains the following functions
You can click on each of them so see what is the purpose and use of them.
In the case of Python, the source code will be saved in a file called noble_1962.py, and we can solve use the code to solve the ODE as follows
import noble_1962 as model
import numpy as np
from scipy.integrate import solve_ivp
import matplotlib.pyplot as plt
T = 5 # Unit is in seconds
# Get default initial state values but add a custom value for V
y = model.init_state_values(V=-86)
# Get default parameter values but add a custom value for Cm
p = model.init_parameter_values(Cm=11)
t = np.linspace(0, T, 1000)
res = solve_ivp(model.rhs, (0, T), y, t_eval=t, method="Radau", args=(p,))
V_index = model.state_index("V")
i_K_index = model.monitor_index("i_K")
monitor = model.monitor_values(res.t, res.y, p)
i_K = monitor[i_K_index, :]
fig, ax = plt.subplots(2, 1, sharex=True)
ax[0].plot(res.t, res.y[V_index, :])
ax[0].set_title("Membrane potential")
ax[1].plot(res.t, i_K)
ax[1].set_title("Potassium current")
plt.show()
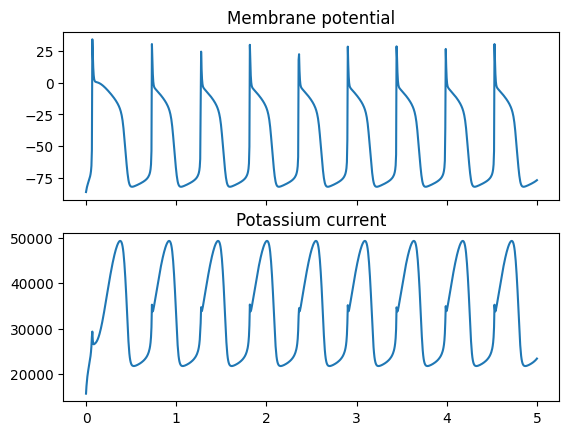
Here we have also used scipy.integrate.solve_ivp for solving the initial value problem.
Generating schemes for ODE#
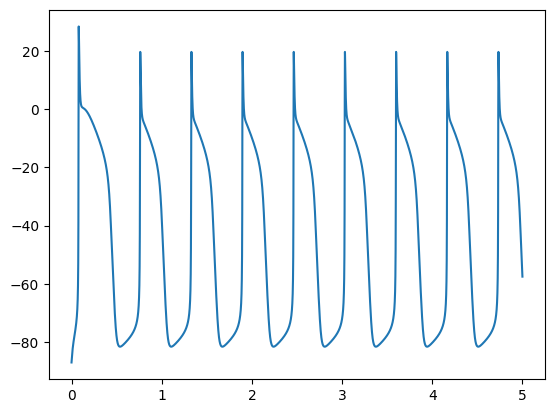
In the example above we only generated the right hand side (function rhs) which can be passed to solve_ivp, but it might be more appropriate to use a specific numerical scheme for solving the ODE. One example of a numerical scheme is the forward euler scheme. Another popular scheme for solving cardiac cell models is the Generalized Rush Larsen scheme.
We can generate this scheme using the following command
!python3 -m gotranx ode2py noble_1962.ode --scheme generalized_rush_larsen -o noble_1962_grl.py
2026-03-04 06:22:30 [info ] Load ode /home/runner/work/gotranx/gotranx/docs/noble_1962.ode
2026-03-04 06:22:30 [info ] Num states 4
2026-03-04 06:22:30 [info ] Num parameters 5
2026-03-04 06:22:31 [info ] Wrote noble_1962_grl.py
Here we also specify that the code should be saved to a new file called noble_1962_grl.py (just to not conflict with the existing file)
The file noble_1962_grl.py will now also contain the function
def generalized_rush_larsen(states, t, dt, parameters): ...
and we can now solve the problem with the following program
import noble_1962_grl as model
import numpy as np
import matplotlib.pyplot as plt
y = model.init_state_values()
p = model.init_parameter_values()
dt = 1e-4 # 0.1 ms
T = 5
t = np.arange(0, T, dt)
V_index = model.state_index("V")
V = [y[V_index]]
for ti in t[1:]:
y = model.generalized_rush_larsen(y, ti, dt, p)
V.append(y[V_index])
plt.plot(t, V)
plt.show()