Endocardial stimulation#
In this demo we show how to load an ODE file and use it to simulate endocardial stimulation.
Fig. 1 Electrode positions#
from collections import defaultdict
from pathlib import Path
import cardiac_geometries
import numpy as np
import matplotlib.pyplot as plt
import dolfin
import pyvista
try:
from tqdm import tqdm
except ImportError:
tqdm = lambda x: x
import beat
import beat.viz
import gotranx
def get_data(datadir="data_endocardial_stimulation"):
datadir = Path(datadir)
msh_file = datadir / "biv_ellipsoid.msh"
if not msh_file.is_file():
cardiac_geometries.create_biv_ellipsoid(
datadir,
char_length=0.2, # Reduce this value to get a finer mesh
center_lv_y=0.2,
center_lv_z=0.0,
a_endo_lv=5.0,
b_endo_lv=2.2,
c_endo_lv=2.2,
a_epi_lv=6.0,
b_epi_lv=3.0,
c_epi_lv=3.0,
center_rv_y=1.0,
center_rv_z=0.0,
a_endo_rv=6.0,
b_endo_rv=2.5,
c_endo_rv=2.7,
a_epi_rv=8.0,
b_epi_rv=5.5,
c_epi_rv=4.0,
create_fibers=True,
)
return cardiac_geometries.geometry.Geometry.from_folder(datadir)
def load_from_file(heart_mesh, xdmffile, key="v", stop_index=None):
V = dolfin.FunctionSpace(heart_mesh, "Lagrange", 1)
v = dolfin.Function(V)
timesteps = beat.postprocess.load_timesteps_from_xdmf(xdmffile)
with dolfin.XDMFFile(Path(xdmffile).as_posix()) as f:
for i, t in tqdm(timesteps.items()):
f.read_checkpoint(v, key, i)
yield v.copy(deepcopy=True), t
def compute_ecg_recovery():
datadir = Path("data_endocardial_stimulation")
xdmffile = datadir / "state.xdmf"
data = get_data(datadir=datadir)
# https://litfl.com/ecg-lead-positioning/
vs = load_from_file(data.mesh, xdmffile, key="V")
leads = dict(
RA=(-15.0, 0.0, -10.0),
LA=(4.0, -12.0, -7.0),
RL=(0.0, 20.0, 3.0),
LL=(17.0, 11.0, 7.0),
V1=(-3.0, 4.0, -9.0),
V2=(0.0, 2.0, -8.0),
V3=(3.0, 1.0, -8.0),
V4=(6.0, 1.0, -6.0),
V5=(10.0, 2.0, 0.0),
V6=(10.0, -6.0, 2.0),
)
fname = datadir / "extracellular_potential.npy"
if not fname.is_file():
phie = defaultdict(list)
time = []
for v, t in vs:
time.append(t)
for name, point in leads.items():
phie[name].append(
beat.ecg.ecg_recovery(v=v, mesh=data.mesh, sigma_b=1.0, point=point)
)
np.save(fname, {"phie": phie, "time": time})
phie_time = np.load(fname, allow_pickle=True).item()
phie = phie_time["phie"]
time = phie_time["time"]
fig, ax = plt.subplots(2, 5, sharex=True, figsize=(12, 8))
for i, (name, values) in enumerate(phie.items()):
axi = ax.flatten()[i]
axi.plot(time, values)
axi.set_title(name)
fig.savefig(datadir / "extracellular_potential.png")
ecg = beat.ecg.Leads12(**{k: np.array(v) for k, v in phie.items()})
fig, ax = plt.subplots(3, 4, sharex=True, figsize=(12, 8))
for i, name in enumerate(
[
"I",
"II",
"III",
"aVR",
"aVL",
"aVF",
"V1_",
"V2_",
"V3_",
"V4_",
"V5_",
"V6_",
]
):
y = getattr(ecg, name)
axi = ax.flatten()[i]
axi.plot(time, y)
axi.set_title(name)
fig.savefig(datadir / "ecg_12_leads.png")
here = Path.cwd()
datadir = here / "data_endocardial_stimulation"
model_path = Path("ORdmm_Land.py")
if not model_path.is_file():
ode = gotranx.load_ode(here / ".." / "odes" / "ORdmm_Land.ode")
code = gotranx.cli.gotran2py.get_code(
ode, scheme=[gotranx.schemes.Scheme.forward_generalized_rush_larsen]
)
model_path.write_text(code)
2025-04-02 20:54:47 [info ] Load ode /__w/fenics-beat/fenics-beat/demos/../odes/ORdmm_Land.ode
2025-04-02 20:54:48 [info ] Num states 48
2025-04-02 20:54:48 [info ] Num parameters 139
import ORdmm_Land
model = ORdmm_Land.__dict__
data = get_data(datadir=datadir)
Calculating scalar fields
Compute scalar laplacian solutions with the markers:
base: [1]
lv: [2]
rv: [3]
epi: [4]
Num vertices: 29407
Num cells: 139200
Calling FFC just-in-time (JIT) compiler, this may take some time.
Calling FFC just-in-time (JIT) compiler, this may take some time.
Calling FFC just-in-time (JIT) compiler, this may take some time.
Calling FFC just-in-time (JIT) compiler, this may take some time.
Calling FFC just-in-time (JIT) compiler, this may take some time.
Calling FFC just-in-time (JIT) compiler, this may take some time.
Calling FFC just-in-time (JIT) compiler, this may take some time.
Apex coord: (7.96, 1.72, -0.05)
Solving Laplace equation
lv = 1, rv, epi = 0
rv = 1, lv, epi = 0
epi = 1, lv, rv = 0
Calling FFC just-in-time (JIT) compiler, this may take some time.
Calculating gradients
Calling FFC just-in-time (JIT) compiler, this may take some time.
Calling FFC just-in-time (JIT) compiler, this may take some time.
Calling FFC just-in-time (JIT) compiler, this may take some time.
Calling FFC just-in-time (JIT) compiler, this may take some time.
Compute fiber-sheet system
Angles:
alpha:
endo_lv: -60
epi_lv: 60
endo_septum: -60
epi_septum: 60
endo_rv: -60
epi_rv: 60
beta:
endo_lv: -65
epi_lv: 25
endo_septum: -65
epi_septum: 25
endo_rv: -65
epi_rv: 25
mesh_unit = "mm"
V = dolfin.FunctionSpace(data.mesh, "Lagrange", 1)
markers = beat.utils.expand_layer_biv(
V=V,
mfun=data.ffun,
endo_lv_marker=data.markers["ENDO_LV"][0],
endo_rv_marker=data.markers["ENDO_RV"][0],
epi_marker=data.markers["EPI"][0],
endo_size=0.3,
epi_size=0.3,
)
pyvista.start_xvfb()
plotter_markers = pyvista.Plotter()
topology, cell_types, x = beat.viz.create_vtk_structures(V)
grid = pyvista.UnstructuredGrid(topology, cell_types, x)
grid["markers"] = markers.vector().get_local()
plotter_markers.add_mesh(grid, show_edges=True)
Actor (0x7fa533439de0)
Center: (3.998753816684164, 1.199999999999994, 0.0)
Pickable: True
Position: (0.0, 0.0, 0.0)
Scale: (1.0, 1.0, 1.0)
Visible: True
X Bounds 0.000E+00, 7.998E+00
Y Bounds -4.300E+00, 6.700E+00
Z Bounds -4.000E+00, 4.000E+00
User matrix: Identity
Has mapper: True
Property (0x7fa53343a140)
Ambient: 0.0
Ambient color: Color(name='lightblue', hex='#add8e6ff', opacity=255)
Anisotropy: 0.0
Color: Color(name='lightblue', hex='#add8e6ff', opacity=255)
Culling: "none"
Diffuse: 1.0
Diffuse color: Color(name='lightblue', hex='#add8e6ff', opacity=255)
Edge color: Color(name='black', hex='#000000ff', opacity=255)
Edge opacity: 1.0
Interpolation: 0
Lighting: True
Line width: 1.0
Metallic: 0.0
Opacity: 1.0
Point size: 5.0
Render lines as tubes: False
Render points as spheres: False
Roughness: 0.5
Show edges: True
Specular: 0.0
Specular color: Color(name='lightblue', hex='#add8e6ff', opacity=255)
Specular power: 100.0
Style: "Surface"
DataSetMapper (0x7fa5334399c0)
Scalar visibility: True
Scalar range: (0.0, 2.0)
Interpolate before mapping: True
Scalar map mode: point
Color mode: map
Attached dataset:
UnstructuredGrid (0x7fa533439a80)
N Cells: 139200
N Points: 29407
X Bounds: 0.000e+00, 7.998e+00
Y Bounds: -4.300e+00, 6.700e+00
Z Bounds: -4.000e+00, 4.000e+00
N Arrays: 1
plotter_markers.view_zy()
plotter_markers.camera.zoom(4)
if not pyvista.OFF_SCREEN:
plotter_markers.show()
else:
figure = plotter_markers.screenshot("fundamentals_mesh.png")
init_states = {
0: model["init_state_values"](),
1: model["init_state_values"](),
2: model["init_state_values"](),
}
# endo = 0, epi = 1, M = 2
parameters = {
0: model["init_parameter_values"](amp=0.0, celltype=2),
1: model["init_parameter_values"](amp=0.0, celltype=0),
2: model["init_parameter_values"](amp=0.0, celltype=1),
}
fun = {
0: model["forward_generalized_rush_larsen"],
1: model["forward_generalized_rush_larsen"],
2: model["forward_generalized_rush_larsen"],
}
v_index = {
0: model["state_index"]("v"),
1: model["state_index"]("v"),
2: model["state_index"]("v"),
}
# Surface to volume ratio
chi = 140.0 * beat.units.ureg("mm**-1")
# Membrane capacitance
C_m = 0.01 * beat.units.ureg("uF/mm**2")
time = dolfin.Constant(0.0)
subdomain_data = dolfin.MeshFunction("size_t", data.mesh, 2)
subdomain_data.set_all(0)
marker = 1
subdomain_data.array()[data.ffun.array() == data.markers["ENDO_LV"][0]] = 1
subdomain_data.array()[data.ffun.array() == data.markers["ENDO_RV"][0]] = 1
I_s = beat.stimulation.define_stimulus(
mesh=data.mesh,
chi=chi,
mesh_unit=mesh_unit,
time=time,
subdomain_data=subdomain_data,
marker=marker,
amplitude=500.0,
)
M = beat.conductivities.define_conductivity_tensor(
chi=chi, f0=data.f0, g_il=0.17, g_it=0.019, g_el=0.62, g_et=0.24
)
params = {"preconditioner": "sor", "use_custom_preconditioner": False}
pde = beat.MonodomainModel(
time=time,
C_m=C_m.to(f"uF/{mesh_unit}**2").magnitude,
mesh=data.mesh,
M=M,
I_s=I_s,
params=params,
)
ode = beat.odesolver.DolfinMultiODESolver(
v_ode=dolfin.Function(V),
v_pde=pde.state,
markers=markers,
num_states={i: len(s) for i, s in init_states.items()},
fun=fun,
init_states=init_states,
parameters=parameters,
v_index=v_index,
)
Calling FFC just-in-time (JIT) compiler, this may take some time.
Calling FFC just-in-time (JIT) compiler, this may take some time.
Calling FFC just-in-time (JIT) compiler, this may take some time.
T = 1
# Change to 500 to simulate the full cardiac cycle
# T = 500
t = 0.0
dt = 0.05
solver = beat.MonodomainSplittingSolver(pde=pde, ode=ode)
fname = (datadir / "state.xdmf").as_posix()
i = 0
while t < T + 1e-12:
if i % 20 == 0:
v = solver.pde.state.vector().get_local()
print(f"Solve for {t=:.2f}, {v.max() =}, {v.min() = }")
with dolfin.XDMFFile(dolfin.MPI.comm_world, fname) as xdmf:
xdmf.parameters["functions_share_mesh"] = True
xdmf.parameters["rewrite_function_mesh"] = False
xdmf.write_checkpoint(
solver.pde.state,
"V",
float(t),
dolfin.XDMFFile.Encoding.HDF5,
True,
)
solver.step((t, t + dt))
i += 1
t += dt
Calling FFC just-in-time (JIT) compiler, this may take some time.
Calling FFC just-in-time (JIT) compiler, this may take some time.
Solve for t=0.00, v.max() =-86.99999999999982, v.min() = -87.00000000000013
Calling FFC just-in-time (JIT) compiler, this may take some time.
Calling FFC just-in-time (JIT) compiler, this may take some time.
Calling FFC just-in-time (JIT) compiler, this may take some time.
Calling FFC just-in-time (JIT) compiler, this may take some time.
Solve for t=1.00, v.max() =-49.021796610832325, v.min() = -91.90071327251552
compute_ecg_recovery()
0%| | 0/2 [00:00<?, ?it/s]
Calling FFC just-in-time (JIT) compiler, this may take some time.
Calling FFC just-in-time (JIT) compiler, this may take some time.
50%|█████ | 1/2 [00:01<00:01, 1.73s/it]
100%|██████████| 2/2 [00:02<00:00, 1.27s/it]
100%|██████████| 2/2 [00:02<00:00, 1.34s/it]
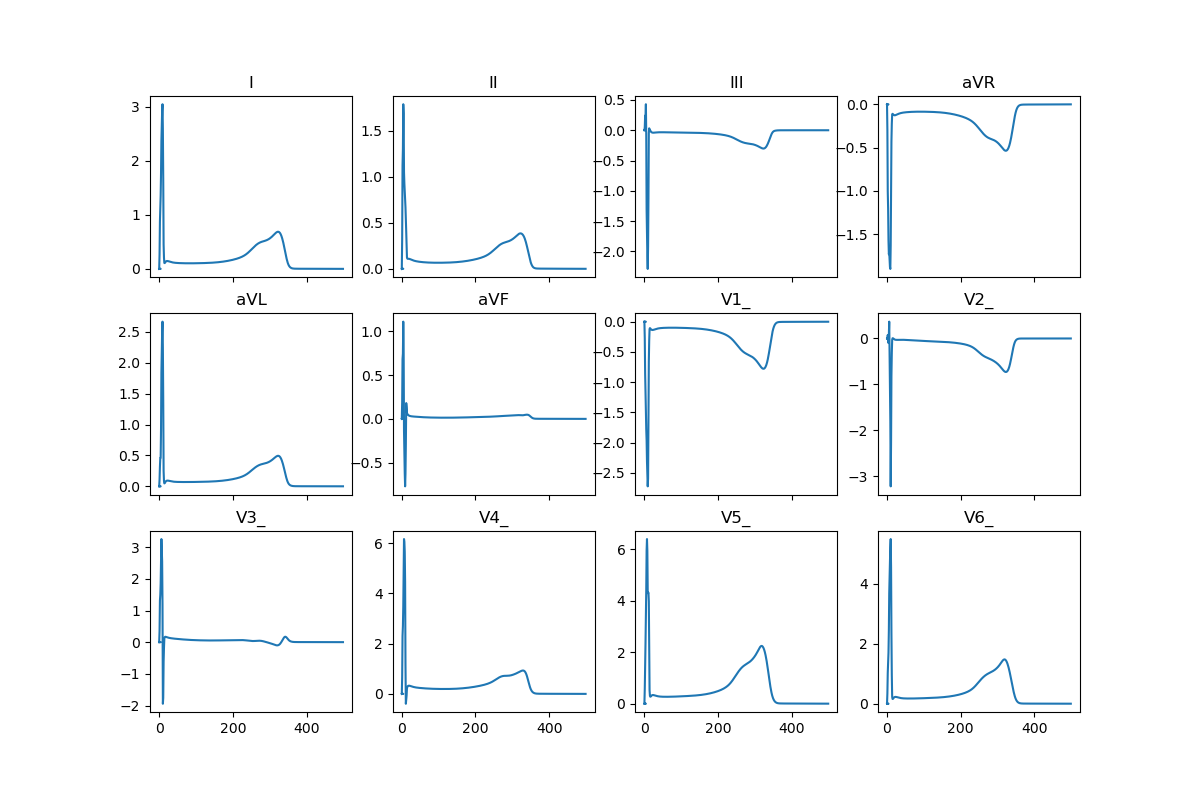
Fig. 2 Precomputed 12-lead ECG#