Your first ODE file#
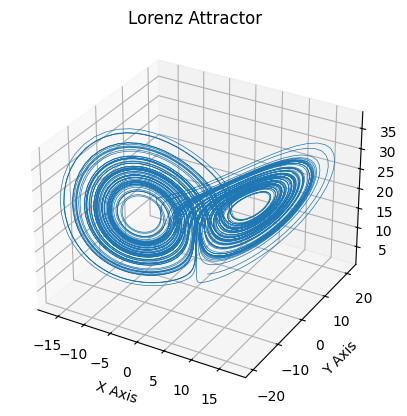
In this tutorial we will show how to write your own ODE file from scratch. We will use Lorentz system as an example. The Lorentz system is a system of ordinary differential equations first studied by Edward Lorenz. It is notable for having chaotic solutions for certain parameter values and initial conditions. In particular, the Lorenz attractor is a set of chaotic solutions of the Lorenz system which, when plotted, resemble a butterfly or figure eight. The equations are given by:
where \(\sigma\), \(\rho\) and \(\beta\) are the parameters of the system.
When solving the system we will use the following parameters:
We will also use the following initial conditions:
Let’s start by writing the ODE file.
ode_str = """
# This is the Lorentz system
# And it is part of this tutorial
parameters(
sigma=12.0,
rho=21.0,
beta=2.4
)
states(x=ScalarParam(1.0, unit="m", description="x variable"), y=2.0,z=3.05)
dx_dt = sigma * (y - x) # The derivative of x
dy_dt = x * (rho - z) - y # m/s
dz_dt = x * y - beta * z
"""
Note that we have also add a description and a unit to the state x, and some description and units to dx_dt and dy_dt respectively. We can now save the file to disk in a file called lorentz.ode and load it with gotranx.load_ode("lorentz.ode"), or we can just create the ODE from a string directly
import gotranx
ode = gotranx.load.ode_from_string(ode_str)
2026-03-04 06:22:52 [info ] Num states 3
2026-03-04 06:22:52 [info ] Num parameters 3
Let us first print the ODE
print(ode)
ODE(ode, num_states=3, num_parameters=3)
We can also print the states
from pprint import pprint
pprint(ode.states)
(State(name='x', components=('',), description='x variable', symbol=x, unit=<Unit('meter')>, value=1.00000000000000),
State(name='y', components=('',), description=None, symbol=y, unit=None, value=2.00000000000000),
State(name='z', components=('',), description=None, symbol=z, unit=None, value=3.05000000000000))
and we see that we have three states. Similarly we can print the parameters
pprint(ode.parameters)
(Parameter(name='beta', components=('',), description=None, symbol=beta, unit=None, value=2.40000000000000),
Parameter(name='rho', components=('',), description=None, symbol=rho, unit=None, value=21.0000000000000),
Parameter(name='sigma', components=('',), description=None, symbol=sigma, unit=None, value=12.0000000000000))
and the state derivatives.
pprint(ode.state_derivatives)
(StateDerivative(name='dx_dt', components=('',), description=None, symbol=dx_dt, unit=None, value=Expression(tree=Tree(Token('RULE', 'term'), [Tree(Token('RULE', 'variable'), [Token('VARIABLE', 'sigma')]), Token('STAR', '*'), Tree(Token('RULE', 'expression'), [Tree(Token('RULE', 'variable'), [Token('VARIABLE', 'y')]), Token('NEG', '-'), Tree(Token('RULE', 'variable'), [Token('VARIABLE', 'x')])])]), dependencies=frozenset({'sigma', 'x', 'y'})), expr=sigma*(-x + y), comment=Comment(text='The derivative of x'), state=State(name='x', components=('',), description='x variable', symbol=x, unit=<Unit('meter')>, value=1.00000000000000)),
StateDerivative(name='dy_dt', components=('',), description=None, symbol=dy_dt, unit=<Unit('meter / second')>, value=Expression(tree=Tree(Token('RULE', 'expression'), [Tree(Token('RULE', 'term'), [Tree(Token('RULE', 'variable'), [Token('VARIABLE', 'x')]), Token('STAR', '*'), Tree(Token('RULE', 'expression'), [Tree(Token('RULE', 'variable'), [Token('VARIABLE', 'rho')]), Token('NEG', '-'), Tree(Token('RULE', 'variable'), [Token('VARIABLE', 'z')])])]), Token('NEG', '-'), Tree(Token('RULE', 'variable'), [Token('VARIABLE', 'y')])]), dependencies=frozenset({'z', 'x', 'rho', 'y'})), expr=x*(rho - z) - y, comment=None, state=State(name='y', components=('',), description=None, symbol=y, unit=None, value=2.00000000000000)),
StateDerivative(name='dz_dt', components=('',), description=None, symbol=dz_dt, unit=None, value=Expression(tree=Tree(Token('RULE', 'expression'), [Tree(Token('RULE', 'term'), [Tree(Token('RULE', 'variable'), [Token('VARIABLE', 'x')]), Token('STAR', '*'), Tree(Token('RULE', 'variable'), [Token('VARIABLE', 'y')])]), Token('NEG', '-'), Tree(Token('RULE', 'term'), [Tree(Token('RULE', 'variable'), [Token('VARIABLE', 'beta')]), Token('STAR', '*'), Tree(Token('RULE', 'variable'), [Token('VARIABLE', 'z')])])]), dependencies=frozenset({'z', 'beta', 'x', 'y'})), expr=-beta*z + x*y, comment=None, state=State(name='z', components=('',), description=None, symbol=z, unit=None, value=3.05000000000000)))
We could also print the intermediates, but there are no intermediate variables (i.e variables that are not states, parameters nor state derivatives) in the model
pprint(ode.intermediates)
()
In the ODE file we also added some text at the top. This can be accessed using the text attribute
print(ode.text)
This is the Lorentz system And it is part of this tutorial
We can also get a dictionary with all the sympy symbols using i the model
print(ode.symbols)
{'rho': rho, 'sigma': sigma, 'beta': beta, 'z': z, 'y': y, 'x': x, 'dz_dt': dz_dt, 'dy_dt': dy_dt, 'dx_dt': dx_dt, 'time': t}
Here the keys are the names of the variables and the values are the sympy symbols. We can also see which variables depend on which variables
print(ode.dependents())
{'z': {'dy_dt', 'dz_dt'}, 'x': {'dx_dt', 'dy_dt', 'dz_dt'}, 'rho': {'dy_dt'}, 'y': {'dx_dt', 'dy_dt', 'dz_dt'}, 'sigma': {'dx_dt'}, 'beta': {'dz_dt'}}
Here for example dz_dt depends only on beta, while all state derivatives depend on the state y. Now let use take a closer look at one of the states, for example x where
x = ode["x"]
print(x)
State(name='x', components=('',), description='x variable', symbol=x, unit=<Unit('meter')>, value=1.00000000000000)
Can print the value
print(x.value)
1.00000000000000
which is actually a sympy object.
print(type(x.value))
<class 'sympy.core.numbers.Float'>
We can also print the unit
print(x.unit)
meter
which is a pint unit object. The original string is stored in the unit_str attribute
print(x.unit_str)
m
Similarly we can print the description
print(x.description)
x variable
and the name and symbol
print(x.name, type(x.name))
print(x.symbol, type(x.symbol))
x <class 'str'>
x <class 'sympy.core.symbol.Symbol'>
For dx_dt we added a comment. This can be accessed using the comment attribute
dx_dt = ode["dx_dt"]
print(dx_dt.comment)
Comment(text='The derivative of x')
Note also that the full tree used when parsing the expression is also saved in the value
print(dx_dt.value.tree.pretty())
term
variable sigma
*
expression
variable y
-
variable x
We can also print the dependencies of the expression
print(dx_dt.value.dependencies)
frozenset({'sigma', 'x', 'y'})
For the state derivatives dy_dt we also added a comment, but this was meant to be a unit. When parsing the comment, gotranx first tries to parse the comment as a unit, and if that fails it will be stored as a comment. We can access the unit using the unit attribute
dy_dt = ode["dy_dt"]
print(dy_dt.unit)
meter / second
Now to generate code can create a code generator object
codegen = gotranx.codegen.PythonCodeGenerator(ode)
and to generate code for the initial states for example we can just call the initial_state_values method
print(codegen.initial_state_values())
def init_state_values(**values):
"""Initialize state values"""
# x=1.0, y=2.0, z=3.05
states = numpy.array([1.0, 2.0, 3.05], dtype=numpy.float64)
for key, value in values.items():
states[state_index(key)] = value
return states
To generate code for a specific scheme you can use the scheme method and pass the scheme and the order of the arguments, for example
print(codegen.scheme(f=gotranx.get_scheme("forward_explicit_euler"), order="stdp"))
def forward_explicit_euler(states, t, dt, parameters):
# Assign states
x = states[0]
y = states[1]
z = states[2]
# Assign parameters
beta = parameters[0]
rho = parameters[1]
sigma = parameters[2]
# Assign expressions
values = numpy.zeros_like(states, dtype=numpy.float64)
dx_dt = sigma * (-x + y)
values[0] = dt * dx_dt + x
dy_dt = x * (rho - z) - y
values[1] = dt * dy_dt + y
dz_dt = -beta * z + x * y
values[2] = dt * dz_dt + z
return values
Note that with this order you get the arguments in the order states, time, dt and parameters. Passing order="ptsd" will give the following order
print(codegen.scheme(f=gotranx.get_scheme("forward_explicit_euler"), order="ptsd"))
def forward_explicit_euler(parameters, t, states, dt):
# Assign states
x = states[0]
y = states[1]
z = states[2]
# Assign parameters
beta = parameters[0]
rho = parameters[1]
sigma = parameters[2]
# Assign expressions
values = numpy.zeros_like(states, dtype=numpy.float64)
dx_dt = sigma * (-x + y)
values[0] = dt * dx_dt + x
dy_dt = x * (rho - z) - y
values[1] = dt * dy_dt + y
dz_dt = -beta * z + x * y
values[2] = dt * dz_dt + z
return values
To list the available schemes you can do
print(gotranx.schemes.list_schemes())
['explicit_euler', 'generalized_rush_larsen', 'forward_explicit_euler', 'forward_generalized_rush_larsen', 'hybrid_rush_larsen']
So let us try to solve it using the forward euler scheme. We can use the gotranx.cli.gotran2py.get_code function to generate the code for all the necessary functions
code = gotranx.cli.gotran2py.get_code(
ode, scheme=[gotranx.schemes.Scheme.forward_explicit_euler]
)
and then execute the code
from typing import Any
model: dict[str, Any] = {}
exec(code, model)
We can now use the model to simulate the system
import numpy as np
import matplotlib.pyplot as plt
y = model["init_state_values"]()
p = model["init_parameter_values"]()
dt = 0.01
t = np.arange(0, 100, dt)
x_index = model["state_index"]("x")
y_index = model["state_index"]("y")
z_index = model["state_index"]("z")
fgr = model["forward_explicit_euler"]
state = np.zeros((3, len(t)))
for i, ti in enumerate(t):
y = fgr(y, ti, dt, p)
state[0, i] = y[x_index]
state[1, i] = y[y_index]
state[2, i] = y[z_index]
And plot the results
fig = plt.figure()
ax = fig.add_subplot(projection="3d")
ax.plot(state[0, :], state[1, :], state[2, :], lw=0.5)
ax.set_xlabel("X Axis")
ax.set_ylabel("Y Axis")
ax.set_zlabel("Z Axis")
ax.set_title("Lorenz Attractor")
plt.show()