A simple example of excitable tissue: The FitzHugh–Nagumo model

The FitzHugh–Nagumo model (FHN), named after Richard FitzHugh (1922–2007) who suggested the system in 1961 and J. Nagumo et al. who created the equivalent circuit the following year, describing a prototype of an excitable system (e.g., a neuron).

The FHN Model is an example of a relaxation oscillator because, if the external stimulus exceeds a certain threshold value, the system will exhibit a characteristic excursion in phase space, before the variables and relax back to their rest values.

This behaviour is typical for spike generations (a short, nonlinear elevation of membrane voltage, diminished over time by a slower, linear recovery variable) in a neuron after stimulation by an external input current.

The equations for this dynamical system read

\[\begin{split} V_{amp} = V_{peak} - V_{rest} \\ I_{Stim} = \begin{cases} stim\_amplitude & \text{if } t \geq stim\_start \text{ and } t \leq stim\_start + stim\_duration \\ 0 & \text{otherwise} \end{cases} \\ \frac{ds}{dt} = b \cdot (-c_3 \cdot s + (V - V_{rest})) \\ V_{th} = V_{amp} \cdot a + V_{rest} \\ I = -s \cdot \left(\frac{c_2}{V_{amp}}\right) \cdot (V - V_{rest}) + \left(\frac{c_1}{V_{amp}^2}\right) \cdot (V - V_{rest}) \cdot (V - V_{th}) \cdot (-V + V_{peak}) \\ \frac{dV}{dt} = I + i_{Stim} \\ \end{split}\]

where \(V\) is the membrane potential, \(s\) is the gating variable, \(V_{rest}\) is the resting potential, \(V_{peak}\) is the peak potential, \(V_{amp}\) is the amplitude of the action potential, \(V_{th}\) is the threshold potential, \(I\) is the current, \(I_{Stim}\) is the external stimulus current, \(a\), \(b\), \(c_1\), \(c_2\), \(c_3\) are parameters, and \(t\) is time.

The FitzHugh–Nagumo model is a simplified version of the Hodgkin–Huxley model, which is a more complex model of the biophysics of the action potential in neurons.

We can formulate the right hand side of the FHN model as a Python function

import numpy as np
from pathlib import Path


def rhs(t, states, parameters):

    # Assign states
    s = states[0]
    V = states[1]

    # Assign parameters
    V_peak = parameters[0]
    V_rest = parameters[1]
    a = parameters[2]
    b = parameters[3]
    c_1 = parameters[4]
    c_2 = parameters[5]
    c_3 = parameters[6]
    stim_amplitude = parameters[7]
    stim_duration = parameters[8]
    stim_start = parameters[9]

    # Assign expressions
    values = np.zeros_like(states, dtype=np.float64)
    V_amp = V_peak - V_rest
    i_Stim = np.where(
        t >= stim_start and t <= stim_start + stim_duration,
        stim_amplitude,
        0,
    )
    ds_dt = b * (-c_3 * s + (V - V_rest))
    values[0] = ds_dt
    V_th = V_amp * a + V_rest
    I = -s * (c_2 / V_amp) * (V - V_rest) + (
        ((c_1 / V_amp**2) * (V - V_rest)) * (V - V_th)
    ) * (-V + V_peak)
    dV_dt = I + i_Stim
    values[1] = dV_dt

    return values

Now, let us pick some parameters and initial conditions

V_peak = 40.0
V_rest = -85.0
a = 0.13
b = 0.013
c_1 = 0.26
c_2 = 0.1
c_3 = 1.0
stim_amplitude = 80.0
stim_duration = 1
stim_start = 1
parameters = np.array(
    [
        V_peak,
        V_rest,
        a,
        b,
        c_1,
        c_2,
        c_3,
        stim_amplitude,
        stim_duration,
        stim_start,
    ],
)
states = np.array([0.0, -85.0])

We can now solve the ODE using a simple explicit Euler method

dt = 0.01
times = np.arange(0, 1000, dt)
all_states = np.zeros((len(times), len(states)))
for i, t in enumerate(times):
    all_states[i, :] = states
    states += rhs(t, states, parameters) * dt

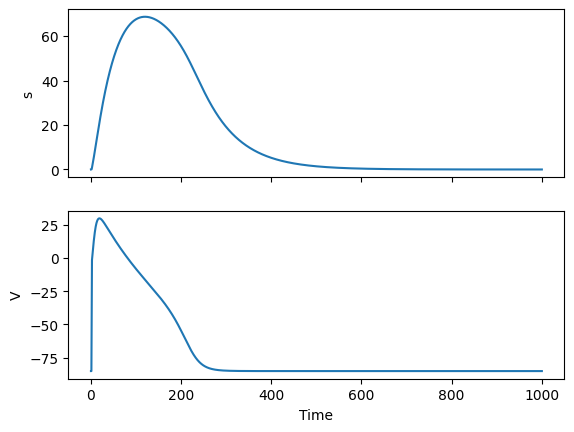
import matplotlib.pyplot as plt

fig, ax = plt.subplots(2, 1, sharex=True)
ax[0].plot(times, all_states[:, 0])
ax[0].set_ylabel("s")
ax[1].plot(times, all_states[:, 1])
ax[1].set_ylabel("V")
ax[1].set_xlabel("Time")
fig.savefig(Path("fitzhughnagumo_0D.png"))

Now, let us solve the FHN model in 2D using FEniCSx and FEniCSx-beat. Let us first create a unit square mesh of size \(10 \times 10\) elements

from mpi4py import MPI
import dolfinx
import ufl
import beat

comm = MPI.COMM_WORLD
N = 10
mesh = dolfinx.mesh.create_unit_square(
    comm,
    N,
    N,
    dolfinx.cpp.mesh.CellType.triangle,
)

# We will also create a variables for the time
time = dolfinx.fem.Constant(mesh, dolfinx.default_scalar_type(0.0))

We can use this time variable to define the external stimulus current which will now be applied to a specific region of the mesh

stim_expr = ufl.conditional(
    ufl.And(ufl.ge(time, stim_start), ufl.le(time, stim_start + stim_duration)),
    stim_amplitude,
    0.0,
)

We will apply the simulus to the lower left corner of the mesh

def stim_region(x):
    return np.logical_and(x[0] <= 0.5, x[1] <= 0.5)


stim_marker = 1
cells = dolfinx.mesh.locate_entities(mesh, mesh.topology.dim, stim_region)
stim_tags = dolfinx.mesh.meshtags(
    mesh,
    mesh.topology.dim,
    cells,
    np.full(len(cells), stim_marker, dtype=np.int32),
)

Now we can create a ufl.Measure which can be used to integrate over the stimulus region

dx = ufl.Measure("dx", domain=mesh, subdomain_data=stim_tags)

We can now define the stimulus current

I_s = beat.Stimulus(expr=stim_expr, dZ=dx, marker=stim_marker)

We also need to make sure to turn off the stimulus current in the ODE solver

parameters[7] = 0.0

We can now define the PDE model.

pde = beat.MonodomainModel(
    time=time,
    mesh=mesh,
    M=0.01,
    I_s=I_s,
    dx=dx,
)

For the ODE model, we first need to define a function that will be used to solve the ODEs. We will use the same function as before in an explicit Euler scheme

def fun(t, states, parameters, dt):
    return states + dt * rhs(t, states, parameters)

We also need to specify a function space for the ODE’s. We will use a simple piecewise linear function space which will solve one ODE per node in the mesh.

ode_space = dolfinx.fem.functionspace(mesh, ("P", 1))
ode = beat.odesolver.DolfinODESolver(
    v_ode=dolfinx.fem.Function(ode_space),
    v_pde=pde.state,
    fun=fun,
    init_states=states,
    parameters=parameters,
    num_states=2,
    v_index=1,
)

Here, we also need to specify the index of the state variable corresponding to the membrane potential, which in our case is the second state variable, with index 1. We combine the PDE and ODE models into a single solver using a splitting scheme

solver = beat.MonodomainSplittingSolver(pde=pde, ode=ode)

Let us set up some way to save the solution to a file. We will use the VTXWriter from FEniCSx where you can visualize the solution using ParaView.

import shutil

shutil.rmtree("fitzhughnagumo.bp", ignore_errors=True)
vtx = dolfinx.io.VTXWriter(
    comm,
    "fitzhughnagumo.bp",
    [solver.pde.state],
    engine="BP4",
)

# We also visualize the solution using PyVista, if available


try:

    import pyvista

except ImportError:

    pyvista = None

else:

    pyvista.start_xvfb()
    plotter = pyvista.Plotter()
    viridis = plt.get_cmap("viridis")
    grid = pyvista.UnstructuredGrid(
        *dolfinx.plot.vtk_mesh(solver.pde.state.function_space.mesh),
    )
    grid.point_data["V"] = solver.pde.state.x.array
    grid.set_active_scalars("V")
    renderer = plotter.add_mesh(
        grid,
        show_edges=True,
        lighting=False,
        cmap=viridis,
        clim=[-90.0, 20.0],
    )
    gif_file = Path("fitzhughnagumo.gif")
    gif_file.unlink(missing_ok=True)
    plotter.view_xy()
    plotter.open_gif(gif_file.as_posix())

# We can now solve the model for a given time interval, say 1000 ms


T = 50
t = 0.0
i = 0
while t < T:
    v = solver.pde.state.x.array
    if i % 20 == 0:
        print(f"Solve for {t=:.2f}, {v.max() =}, {v.min() =}")
        vtx.write(t)
        if pyvista:
            grid.point_data["V"] = solver.pde.state.x.array
            plotter.write_frame()

    solver.step((t, t + dt))
    i += 1
    t += dt

vtx.close()
if pyvista:
    plotter.close()

Solve for t=0.00, v.max() =np.float64(-84.99999999997898), v.min() =np.float64(-84.99999999997898)
Solve for t=0.20, v.max() =np.float64(-84.99028802811642), v.min() =np.float64(-85.00525255359862)
Solve for t=0.40, v.max() =np.float64(-84.98778441891083), v.min() =np.float64(-85.0073416852096)
Solve for t=0.60, v.max() =np.float64(-84.98698603628776), v.min() =np.float64(-85.00857753701652)
Solve for t=0.80, v.max() =np.float64(-84.9868875300404), v.min() =np.float64(-85.01004090636053)
Solve for t=1.00, v.max() =np.float64(-84.9871334431899), v.min() =np.float64(-85.01131837570736)

error: XDG_RUNTIME_DIR is invalid or not set in the environment.

Solve for t=1.20, v.max() =np.float64(-67.94135578097902), v.min() =np.float64(-85.53198603713496)
Solve for t=1.40, v.max() =np.float64(-52.41358947828942), v.min() =np.float64(-85.64208220980824)
Solve for t=1.60, v.max() =np.float64(-36.18006692065493), v.min() =np.float64(-85.3847928763925)
Solve for t=1.80, v.max() =np.float64(-19.92259090228013), v.min() =np.float64(-85.3392619920787)
Solve for t=2.00, v.max() =np.float64(-3.2061967815225922), v.min() =np.float64(-85.24717611278211)
Solve for t=2.20, v.max() =np.float64(-2.546518550084846), v.min() =np.float64(-85.29753186038334)

Solve for t=2.40, v.max() =np.float64(-1.747044768955156), v.min() =np.float64(-85.18098423634315)
Solve for t=2.60, v.max() =np.float64(-0.9499497116979925), v.min() =np.float64(-85.16194543597544)
Solve for t=2.80, v.max() =np.float64(-0.11369079151731373), v.min() =np.float64(-85.12014536684664)
Solve for t=3.00, v.max() =np.float64(0.5835365818122182), v.min() =np.float64(-85.09340137141275)
Solve for t=3.20, v.max() =np.float64(1.0912646733172127), v.min() =np.float64(-85.09260428624619)
Solve for t=3.40, v.max() =np.float64(1.3990922944303315), v.min() =np.float64(-85.08379866286579)

Solve for t=3.60, v.max() =np.float64(1.5195412368982506), v.min() =np.float64(-85.0739486958742)
Solve for t=3.80, v.max() =np.float64(1.475272739804934), v.min() =np.float64(-85.06179792497917)
Solve for t=4.00, v.max() =np.float64(1.2917232323609067), v.min() =np.float64(-85.05955943116516)
Solve for t=4.20, v.max() =np.float64(0.9934053019953868), v.min() =np.float64(-85.06510522000065)
Solve for t=4.40, v.max() =np.float64(0.6023068280678344), v.min() =np.float64(-85.06562820944218)
Solve for t=4.60, v.max() =np.float64(0.13739275054197259), v.min() =np.float64(-85.0560630535652)

Solve for t=4.80, v.max() =np.float64(-0.3853554093689725), v.min() =np.float64(-85.03554247245042)
Solve for t=5.00, v.max() =np.float64(-0.952664961785391), v.min() =np.float64(-85.00363667423551)
Solve for t=5.20, v.max() =np.float64(-1.5536175816655768), v.min() =np.float64(-84.96024596167554)
Solve for t=5.40, v.max() =np.float64(-2.179290421276803), v.min() =np.float64(-84.90551164571228)
Solve for t=5.60, v.max() =np.float64(-2.8224263610515807), v.min() =np.float64(-84.83974490098052)
Solve for t=5.80, v.max() =np.float64(-3.4771455857085654), v.min() =np.float64(-84.76337140520683)
Solve for t=6.00, v.max() =np.float64(-4.138700228872757), v.min() =np.float64(-84.67688912167034)

Solve for t=6.20, v.max() =np.float64(-4.80326910103957), v.min() =np.float64(-84.58083667800457)
Solve for t=6.40, v.max() =np.float64(-5.467787706664541), v.min() =np.float64(-84.47577010941244)
Solve for t=6.60, v.max() =np.float64(-6.129808383891617), v.min() =np.float64(-84.362246103943)
Solve for t=6.80, v.max() =np.float64(-6.787385689526693), v.min() =np.float64(-84.24081023963923)
Solve for t=7.00, v.max() =np.float64(-7.438982704843713), v.min() =np.float64(-84.11198901115854)
Solve for t=7.20, v.max() =np.float64(-8.083394557581835), v.min() =np.float64(-83.97628470070417)

Solve for t=7.40, v.max() =np.float64(-8.71968604997509), v.min() =np.float64(-83.8341723575579)
Solve for t=7.60, v.max() =np.float64(-9.347140813824991), v.min() =np.float64(-83.68609831832568)
Solve for t=7.80, v.max() =np.float64(-9.965219870451492), v.min() =np.float64(-83.53247983290844)
Solve for t=8.00, v.max() =np.float64(-10.573527857586358), v.min() =np.float64(-83.3737054656416)
Solve for t=8.20, v.max() =np.float64(-11.171785504089579), v.min() =np.float64(-83.21013602250405)
Solve for t=8.40, v.max() =np.float64(-11.759807195682205), v.min() =np.float64(-83.0421058184907)

Solve for t=8.60, v.max() =np.float64(-12.337482689589024), v.min() =np.float64(-82.86992414795102)
Solve for t=8.80, v.max() =np.float64(-12.904762211142266), v.min() =np.float64(-82.69387685804631)
Solve for t=9.00, v.max() =np.float64(-13.461644308026237), v.min() =np.float64(-82.51422795392081)
Solve for t=9.20, v.max() =np.float64(-14.008165953866206), v.min() =np.float64(-82.3312211856969)
Solve for t=9.40, v.max() =np.float64(-14.54439448719556), v.min() =np.float64(-82.14508158355086)
Solve for t=9.60, v.max() =np.float64(-15.070421048529784), v.min() =np.float64(-81.95601691912628)

Solve for t=9.80, v.max() =np.float64(-15.586355240635207), v.min() =np.float64(-81.76421908035147)
Solve for t=10.00, v.max() =np.float64(-16.092320787807683), v.min() =np.float64(-81.56986535313831)
Solve for t=10.20, v.max() =np.float64(-16.588452011251952), v.min() =np.float64(-81.37311960796248)
Solve for t=10.40, v.max() =np.float64(-17.074890971258935), v.min() =np.float64(-81.17413339250466)
Solve for t=10.60, v.max() =np.float64(-17.55178515425321), v.min() =np.float64(-80.97304693364086)
Solve for t=10.80, v.max() =np.float64(-18.019285605093643), v.min() =np.float64(-80.76999005342901)

Solve for t=11.00, v.max() =np.float64(-18.477545423204504), v.min() =np.float64(-80.56508300452839)
Solve for t=11.20, v.max() =np.float64(-18.926718555957727), v.min() =np.float64(-80.35843723087143)
Solve for t=11.40, v.max() =np.float64(-19.366958834847406), v.min() =np.float64(-80.15015605951203)
Solve for t=11.60, v.max() =np.float64(-19.798419209893368), v.min() =np.float64(-79.94033532947033)
Solve for t=11.80, v.max() =np.float64(-20.221251145799403), v.min() =np.float64(-79.72906396317067)
Solve for t=12.00, v.max() =np.float64(-20.63560415000509), v.min() =np.float64(-79.51642448575313)

Solve for t=12.20, v.max() =np.float64(-21.041625408177616), v.min() =np.float64(-79.30249349718265)
Solve for t=12.40, v.max() =np.float64(-21.439459507117654), v.min() =np.float64(-79.08734210170088)
Solve for t=12.60, v.max() =np.float64(-21.829248228673805), v.min() =np.float64(-78.8710362987835)
Solve for t=12.80, v.max() =np.float64(-22.211130401231788), v.min() =np.float64(-78.6536373393897)
Solve for t=13.00, v.max() =np.float64(-22.585241797769694), v.min() =np.float64(-78.43520205093499)
Solve for t=13.20, v.max() =np.float64(-22.951715071469838), v.min() =np.float64(-78.21578313408277)
Solve for t=13.40, v.max() =np.float64(-23.31067972150422), v.min() =np.float64(-77.9954294341421)

Solve for t=13.60, v.max() =np.float64(-23.662262082955657), v.min() =np.float64(-77.7741861895642)
Solve for t=13.80, v.max() =np.float64(-24.006585335932204), v.min() =np.float64(-77.55209525978495)
Solve for t=14.00, v.max() =np.float64(-24.343769529834166), v.min() =np.float64(-77.32919533440909)
Solve for t=14.20, v.max() =np.float64(-24.673931619473535), v.min() =np.float64(-77.1055221255322)
Solve for t=14.40, v.max() =np.float64(-24.99718551035244), v.min() =np.float64(-76.88110854479855)
Solve for t=14.60, v.max() =np.float64(-25.313642110905807), v.min() =np.float64(-76.65598486662476)

Solve for t=14.80, v.max() =np.float64(-25.62340938992044), v.min() =np.float64(-76.43017887887207)
Solve for t=15.00, v.max() =np.float64(-25.926592437681734), v.min() =np.float64(-76.20371602210245)
Solve for t=15.20, v.max() =np.float64(-26.223293529671743), v.min() =np.float64(-75.97661951844833)
Solve for t=15.40, v.max() =np.float64(-26.513612191870923), v.min() =np.float64(-75.74891049100961)
Solve for t=15.60, v.max() =np.float64(-26.79764526689786), v.min() =np.float64(-75.52060807459559)
Solve for t=15.80, v.max() =np.float64(-27.07548698037869), v.min() =np.float64(-75.29172951855423)

Solve for t=16.00, v.max() =np.float64(-27.347229007056487), v.min() =np.float64(-75.06229028234881)
Solve for t=16.20, v.max() =np.float64(-27.612960536257795), v.min() =np.float64(-74.83230412447695)
Solve for t=16.40, v.max() =np.float64(-27.872768336415675), v.min() =np.float64(-74.60178318526864)
Solve for t=16.60, v.max() =np.float64(-28.12673681841409), v.min() =np.float64(-74.37073806405367)
Solve for t=16.80, v.max() =np.float64(-28.374948097579786), v.min() =np.float64(-74.13917789113128)
Solve for t=17.00, v.max() =np.float64(-28.617482054187967), v.min() =np.float64(-73.90711039494275)

Solve for t=17.20, v.max() =np.float64(-28.85441639238804), v.min() =np.float64(-73.6745419648065)
Solve for t=17.40, v.max() =np.float64(-29.085826697485352), v.min() =np.float64(-73.44147770954356)
Solve for t=17.60, v.max() =np.float64(-29.311786491538218), v.min() =np.float64(-73.20792151229399)
Solve for t=17.80, v.max() =np.float64(-29.532367287249006), v.min() =np.float64(-72.97387608179257)
Solve for t=18.00, v.max() =np.float64(-29.7476386401461), v.min() =np.float64(-72.73934300035778)
Solve for t=18.20, v.max() =np.float64(-29.95766819906232), v.min() =np.float64(-72.50432276881716)

Solve for t=18.40, v.max() =np.float64(-30.16252175492833), v.min() =np.float64(-72.2688148485821)
Solve for t=18.60, v.max() =np.float64(-30.36226328790657), v.min() =np.float64(-72.03281770106047)
Solve for t=18.80, v.max() =np.float64(-30.55695501289611), v.min() =np.float64(-71.79632882458647)
Solve for t=19.00, v.max() =np.float64(-30.746657423444347), v.min() =np.float64(-71.55934478902863)
Solve for t=19.20, v.max() =np.float64(-30.931429334105832), v.min() =np.float64(-71.32186126822538)
Solve for t=19.40, v.max() =np.float64(-31.111327921288257), v.min() =np.float64(-71.08387307039057)

Solve for t=19.60, v.max() =np.float64(-31.286408762631282), v.min() =np.float64(-70.84537416661213)
Solve for t=19.80, v.max() =np.float64(-31.456725874959773), v.min() =np.float64(-70.60635771756644)
Solve for t=20.00, v.max() =np.float64(-31.62233175085904), v.min() =np.float64(-70.36681609855907)
Solve for t=20.20, v.max() =np.float64(-31.78327739391715), v.min() =np.float64(-70.12674092299123)
Solve for t=20.40, v.max() =np.float64(-31.9396123526767), v.min() =np.float64(-69.88612306435061)
Solve for t=20.60, v.max() =np.float64(-32.09138475334367), v.min() =np.float64(-69.6449526768134)
Solve for t=20.80, v.max() =np.float64(-32.23864133129584), v.min() =np.float64(-69.40321921454232)

Solve for t=21.00, v.max() =np.float64(-32.38142746143511), v.min() =np.float64(-69.16091144975742)
Solve for t=21.20, v.max() =np.float64(-32.51978718742409), v.min() =np.float64(-68.91801748965062)
Solve for t=21.40, v.max() =np.float64(-32.653763249850506), v.min() =np.float64(-68.6745247922145)
Solve for t=21.60, v.max() =np.float64(-32.783397113358966), v.min() =np.float64(-68.43042018104704)
Solve for t=21.80, v.max() =np.float64(-32.908728992788404), v.min() =np.float64(-68.18568985919389)
Solve for t=22.00, v.max() =np.float64(-33.029797878354486), v.min() =np.float64(-67.94031942208024)
Solve for t=22.20, v.max() =np.float64(-33.14664155991456), v.min() =np.float64(-67.69429386959263)

Solve for t=22.40, v.max() =np.float64(-33.25929665034966), v.min() =np.float64(-67.44759761735197)
Solve for t=22.60, v.max() =np.float64(-33.367798608098724), v.min() =np.float64(-67.20021450723098)
Solve for t=22.80, v.max() =np.float64(-33.472181758880794), v.min() =np.float64(-66.95212781715797)
Solve for t=23.00, v.max() =np.float64(-33.572479316634166), v.min() =np.float64(-66.70332027025047)
Solve for t=23.20, v.max() =np.float64(-33.668723403709095), v.min() =np.float64(-66.45377404331592)
Solve for t=23.40, v.max() =np.float64(-33.760945070340775), v.min() =np.float64(-66.20347077476148)

Solve for t=23.60, v.max() =np.float64(-33.84917431343325), v.min() =np.float64(-65.95239157194501)
Solve for t=23.80, v.max() =np.float64(-33.93344009468596), v.min() =np.float64(-65.70051701800556)
Solve for t=24.00, v.max() =np.float64(-34.013770358086866), v.min() =np.float64(-65.44782717820259)
Solve for t=24.20, v.max() =np.float64(-34.090192046801945), v.min() =np.float64(-65.19430160579796)
Solve for t=24.40, v.max() =np.float64(-34.162731119488136), v.min() =np.float64(-64.93991934751224)
Solve for t=24.60, v.max() =np.float64(-34.23141256605132), v.min() =np.float64(-64.68465894857856)

Solve for t=24.80, v.max() =np.float64(-34.29626042287945), v.min() =np.float64(-64.4284984574301)
Solve for t=25.00, v.max() =np.float64(-34.357297787572534), v.min() =np.float64(-64.1714154300425)
Solve for t=25.20, v.max() =np.float64(-34.41454683319168), v.min() =np.float64(-63.913386933958805)
Solve for t=25.40, v.max() =np.float64(-34.468028822052794), v.min() =np.float64(-63.65438955202572)
Solve for t=25.60, v.max() =np.float64(-34.51776411908773), v.min() =np.float64(-63.39439938586275)
Solve for t=25.80, v.max() =np.float64(-34.56377220479143), v.min() =np.float64(-63.133392059088465)

Solve for t=26.00, v.max() =np.float64(-34.60607168778059), v.min() =np.float64(-62.87134272033116)
Solve for t=26.20, v.max() =np.float64(-34.64468031698264), v.min() =np.float64(-62.6082260460448)
Solve for t=26.40, v.max() =np.float64(-34.67961499347589), v.min() =np.float64(-62.34401624315358)
Solve for t=26.60, v.max() =np.float64(-34.710891782002626), v.min() =np.float64(-62.07868705155139)
Solve for t=26.80, v.max() =np.float64(-34.738525922173615), v.min() =np.float64(-61.8122117464747)
Solve for t=27.00, v.max() =np.float64(-34.76253183938444), v.min() =np.float64(-61.54456314077352)
Solve for t=27.20, v.max() =np.float64(-34.78292315546388), v.min() =np.float64(-61.27571358710651)

Solve for t=27.40, v.max() =np.float64(-34.79971269907251), v.min() =np.float64(-61.00563498007752)
Solve for t=27.60, v.max() =np.float64(-34.812912515871716), v.min() =np.float64(-60.73429875834078)
Solve for t=27.80, v.max() =np.float64(-34.8225338784811), v.min() =np.float64(-60.4616759066961)
Solve for t=28.00, v.max() =np.float64(-34.82858729624526), v.min() =np.float64(-60.18773695819931)
Solve for t=28.20, v.max() =np.float64(-34.83108252482639), v.min() =np.float64(-59.912451996310054)
Solve for t=28.40, v.max() =np.float64(-34.83002857564385), v.min() =np.float64(-59.63579065710114)
Solve for t=28.60, v.max() =np.float64(-34.82543372517775), v.min() =np.float64(-59.357722131556564)

Solve for t=28.80, v.max() =np.float64(-34.81730552415761), v.min() =np.float64(-59.07821516798033)
Solve for t=29.00, v.max() =np.float64(-34.805650806653006), v.min() =np.float64(-58.797238074543834)
Solve for t=29.20, v.max() =np.float64(-34.79047569908741), v.min() =np.float64(-58.514758721997694)
Solve for t=29.40, v.max() =np.float64(-34.77178562919365), v.min() =np.float64(-58.23074454657479)
Solve for t=29.60, v.max() =np.float64(-34.74958533493046), v.min() =np.float64(-57.94516255311387)
Solve for t=29.80, v.max() =np.float64(-34.72387887337993), v.min() =np.float64(-57.65797931842995)

Solve for t=30.00, v.max() =np.float64(-34.69466962964709), v.min() =np.float64(-57.36916099496255)
Solve for t=30.20, v.max() =np.float64(-34.661960325780655), v.min() =np.float64(-57.078673314733834)
Solve for t=30.40, v.max() =np.float64(-34.62575302973593), v.min() =np.float64(-56.78648159364525)
Solve for t=30.60, v.max() =np.float64(-34.58604916440219), v.min() =np.float64(-56.49255073614602)
Solve for t=30.80, v.max() =np.float64(-34.542849516713176), v.min() =np.float64(-56.19684524030964)
Solve for t=31.00, v.max() =np.float64(-34.49615424686689), v.min() =np.float64(-55.899329203349964)
Solve for t=31.20, v.max() =np.float64(-34.44596289767304), v.min() =np.float64(-55.5999663276147)

Solve for t=31.40, v.max() =np.float64(-34.392274404053246), v.min() =np.float64(-55.29871992709467)
Solve for t=31.60, v.max() =np.float64(-34.33508710271665), v.min() =np.float64(-54.995552934484515)
Solve for t=31.80, v.max() =np.float64(-34.27439874203584), v.min() =np.float64(-54.690427908839546)
Solve for t=32.00, v.max() =np.float64(-34.21020649214579), v.min() =np.float64(-54.38330704386483)
Solve for t=32.20, v.max() =np.float64(-34.14250695529337), v.min() =np.float64(-54.07415217688572)
Solve for t=32.40, v.max() =np.float64(-34.071296176461296), v.min() =np.float64(-53.762924798539565)

Solve for t=32.60, v.max() =np.float64(-33.996569654293815), v.min() =np.float64(-53.449586063237994)
Solve for t=32.80, v.max() =np.float64(-33.91832235235239), v.min() =np.float64(-53.134096800446066)
Solve for t=33.00, v.max() =np.float64(-33.83654871072704), v.min() =np.float64(-52.816417526829134)
Solve for t=33.20, v.max() =np.float64(-33.75124265803398), v.min() =np.float64(-52.49650845931875)
Solve for t=33.40, v.max() =np.float64(-33.662397623828525), v.min() =np.float64(-52.174329529149425)
Solve for t=33.60, v.max() =np.float64(-33.5700065514635), v.min() =np.float64(-51.84984039692354)

Solve for t=33.80, v.max() =np.float64(-33.47406191142341), v.min() =np.float64(-51.523000468759975)
Solve for t=34.00, v.max() =np.float64(-33.37455571516902), v.min() =np.float64(-51.19376891358469)
Solve for t=34.20, v.max() =np.float64(-33.271479529521386), v.min() =np.float64(-50.86210468162553)
Solve for t=34.40, v.max() =np.float64(-33.16482449162238), v.min() =np.float64(-50.52796652417151)
Solve for t=34.60, v.max() =np.float64(-33.05458132450438), v.min() =np.float64(-50.191313014663564)
Solve for t=34.80, v.max() =np.float64(-32.94074035330529), v.min() =np.float64(-49.852102571180524)

Solve for t=35.00, v.max() =np.float64(-32.823291522165164), v.min() =np.float64(-49.51029348039017)
Solve for t=35.20, v.max() =np.float64(-32.70222441184182), v.min() =np.float64(-49.16584392303384)
Solve for t=35.40, v.max() =np.float64(-32.57752825808326), v.min() =np.float64(-48.8187120010179)
Solve for t=35.60, v.max() =np.float64(-32.449191970796264), v.min() =np.float64(-48.46885576618353)
Solve for t=35.80, v.max() =np.float64(-32.317204154050195), v.min() =np.float64(-48.116233250830675)
Solve for t=36.00, v.max() =np.float64(-32.181553126959294), v.min() =np.float64(-47.76080250007362)
Solve for t=36.20, v.max() =np.float64(-32.04222694548122), v.min() =np.float64(-47.40252160610492)

Solve for t=36.40, v.max() =np.float64(-31.89921342517705), v.min() =np.float64(-47.041348744447106)
Solve for t=36.60, v.max() =np.float64(-31.75250016497537), v.min() =np.float64(-46.677242212273086)
Solve for t=36.80, v.max() =np.float64(-31.60207457198318), v.min() =np.float64(-46.31016046887676)
Solve for t=37.00, v.max() =np.float64(-31.447923887388765), v.min() =np.float64(-45.94006217837618)
Solve for t=37.20, v.max() =np.float64(-31.290035213502236), v.min() =np.float64(-45.56690625473136)
Solve for t=37.40, v.max() =np.float64(-31.128395541977937), v.min() =np.float64(-45.19065190916126)

Solve for t=37.60, v.max() =np.float64(-30.962991783265394), v.min() =np.float64(-44.8112587000431)
Solve for t=37.80, v.max() =np.float64(-30.793810797335258), v.min() =np.float64(-44.42868658537558)
Solve for t=38.00, v.max() =np.float64(-30.62083942572569), v.min() =np.float64(-44.0428959778906)
Solve for t=38.20, v.max() =np.float64(-30.4440645249584), v.min() =np.float64(-43.6538478028944)
Solve for t=38.40, v.max() =np.float64(-30.263473001366638), v.min() =np.float64(-43.26150355891792)
Solve for t=38.60, v.max() =np.float64(-30.079051847386165), v.min() =np.float64(-42.86582538125616)
Solve for t=38.80, v.max() =np.float64(-29.890788179350963), v.min() =np.float64(-42.46677610847063)

Solve for t=39.00, v.max() =np.float64(-29.698669276843127), v.min() =np.float64(-42.06431935193071)
Solve for t=39.20, v.max() =np.float64(-29.50268262363788), v.min() =np.float64(-41.65841956846247)
Solve for t=39.40, v.max() =np.float64(-29.30281595029114), v.min() =np.float64(-41.24904213617067)
Solve for t=39.60, v.max() =np.float64(-29.09905727840875), v.min() =np.float64(-40.83615343349649)
Solve for t=39.80, v.max() =np.float64(-28.891394966641645), v.min() =np.float64(-40.419720921564526)
Solve for t=40.00, v.max() =np.float64(-28.67981775844428), v.min() =np.float64(-39.99971322987173)
Solve for t=40.20, v.max() =np.float64(-28.46431483163504), v.min() =np.float64(-39.5761002453563)

Solve for t=40.40, v.max() =np.float64(-28.244875849792887), v.min() =np.float64(-39.1488532048859)
Solve for t=40.60, v.max() =np.float64(-28.021491015522976), v.min() =np.float64(-38.71794479118619)
Solve for t=40.80, v.max() =np.float64(-27.794151125621653), v.min() =np.float64(-38.283349232228794)
Solve for t=41.00, v.max() =np.float64(-27.56284762816466), v.min() =np.float64(-37.84504240407991)
Solve for t=41.20, v.max() =np.float64(-27.327572681543597), v.min() =np.float64(-37.40300193720582)
Solve for t=41.40, v.max() =np.float64(-27.08831921546564), v.min() =np.float64(-36.95720732621092)

Solve for t=41.60, v.max() =np.float64(-26.845080993931855), v.min() =np.float64(-36.50764004297542)
Solve for t=41.80, v.max() =np.float64(-26.597852680201083), v.min() =np.float64(-36.05428365314024)
Solve for t=42.00, v.max() =np.float64(-26.34662990374183), v.min() =np.float64(-35.59712393587347)
Solve for t=42.20, v.max() =np.float64(-26.09140932916785), v.min() =np.float64(-35.13614900682795)
Solve for t=42.40, v.max() =np.float64(-25.832188727147), v.min() =np.float64(-34.67134944418885)
Solve for t=42.60, v.max() =np.float64(-25.568967047265268), v.min() =np.float64(-34.20271841768036)
Solve for t=42.80, v.max() =np.float64(-25.30174449281873), v.min() =np.float64(-33.730251820384154)

Solve for t=43.00, v.max() =np.float64(-25.030522597499193), v.min() =np.float64(-33.25394840319445)
Solve for t=43.20, v.max() =np.float64(-24.755304303930085), v.min() =np.float64(-32.77380991171301)
Solve for t=43.40, v.max() =np.float64(-24.476094043996675), v.min() =np.float64(-32.289841225356184)
Solve for t=43.60, v.max() =np.float64(-24.192897820907383), v.min() =np.float64(-31.802050498422055)
Solve for t=43.80, v.max() =np.float64(-23.905723292910125), v.min() =np.float64(-31.31044930283511)
Solve for t=44.00, v.max() =np.float64(-23.614579858575702), v.min() =np.float64(-30.815052772253548)

Solve for t=44.20, v.max() =np.float64(-23.31947874354644), v.min() =np.float64(-30.31587974719544)
Solve for t=44.40, v.max() =np.float64(-23.02043308863898), v.min() =np.float64(-29.812952920804936)
Solve for t=44.60, v.max() =np.float64(-22.71745803917113), v.min() =np.float64(-29.30629898484806)
Solve for t=44.80, v.max() =np.float64(-22.410570835371374), v.min() =np.float64(-28.795948775489762)
Solve for t=45.00, v.max() =np.float64(-22.09979090371332), v.min() =np.float64(-28.281937418373253)
Solve for t=45.20, v.max() =np.float64(-21.78513994900173), v.min() =np.float64(-27.764304472483083)

Solve for t=45.40, v.max() =np.float64(-21.46664204702018), v.min() =np.float64(-27.243094072240293)
Solve for t=45.60, v.max() =np.float64(-21.144323737533902), v.min() =np.float64(-26.718355067240754)
Solve for t=45.80, v.max() =np.float64(-20.818214117422865), v.min() =np.float64(-26.19014115901276)
Solve for t=46.00, v.max() =np.float64(-20.488344933704244), v.min() =np.float64(-25.65851103413683)
Solve for t=46.20, v.max() =np.float64(-20.154750676183532), v.min() =np.float64(-25.123528493033096)
Solve for t=46.40, v.max() =np.float64(-19.81746866945571), v.min() =np.float64(-24.58526257369394)

Solve for t=46.60, v.max() =np.float64(-19.476539163961007), v.min() =np.float64(-24.043787669604793)
Solve for t=46.80, v.max() =np.float64(-19.132005425777567), v.min() =np.float64(-23.499183641069962)
Solve for t=47.00, v.max() =np.float64(-18.783913824819653), v.min() =np.float64(-22.951535919132848)
Solve for t=47.20, v.max() =np.float64(-18.432313921087367), v.min() =np.float64(-22.400935601257842)
Solve for t=47.40, v.max() =np.float64(-18.07725854859955), v.min() =np.float64(-21.84747953792108)
Solve for t=47.60, v.max() =np.float64(-17.71880389662111), v.min() =np.float64(-21.29127040924143)
Solve for t=47.80, v.max() =np.float64(-17.357009587781896), v.min() =np.float64(-20.73241679077308)

Solve for t=48.00, v.max() =np.float64(-16.99193875266714), v.min() =np.float64(-20.17103320757373)
Solve for t=48.20, v.max() =np.float64(-16.623658100444814), v.min() =np.float64(-19.607240175662913)
Solve for t=48.40, v.max() =np.float64(-16.25223798508171), v.min() =np.float64(-19.04116422998897)
Solve for t=48.60, v.max() =np.float64(-15.877752466688179), v.min() =np.float64(-18.47293793803631)
Solve for t=48.80, v.max() =np.float64(-15.442037518843362), v.min() =np.float64(-17.902699898221933)
Solve for t=49.00, v.max() =np.float64(-14.983946718848038), v.min() =np.float64(-17.330594722257473)

Solve for t=49.20, v.max() =np.float64(-14.514043688596786), v.min() =np.float64(-16.756773000685385)
Solve for t=49.40, v.max() =np.float64(-14.036733585672883), v.min() =np.float64(-16.181391250839933)
Solve for t=49.60, v.max() =np.float64(-13.557681925451547), v.min() =np.float64(-15.604611846533698)
Solve for t=49.80, v.max() =np.float64(-13.07701373665444), v.min() =np.float64(-15.026602928828206)
Solve for t=50.00, v.max() =np.float64(-12.593471359220285), v.min() =np.float64(-14.447538297314471)