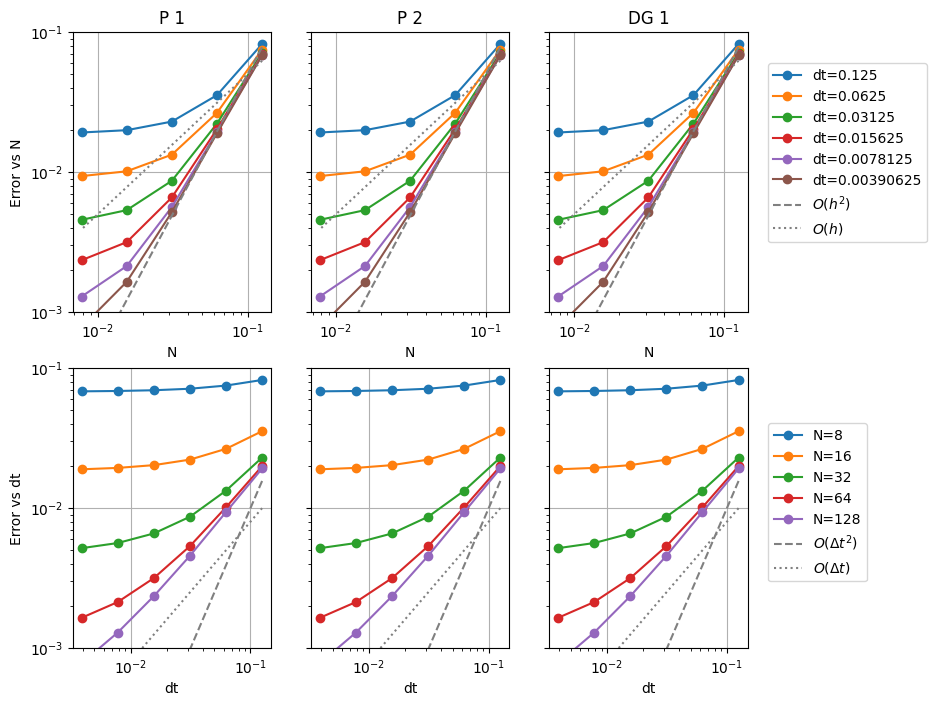
Monodomain convergence test

In this example, we will demonstrate how to perform a convergence test for the monodomain model using the forward Euler method for the ODE solver. We will use the same test case as in the tests/test_monodomain.py file. We will compare the error in the solution for different spatial and temporal resolutions. We will use the L2 norm of the error as the error measure.

from collections import defaultdict
import ufl
import json
from pathlib import Path
import numpy as np
import matplotlib.pyplot as plt
from mpi4py import MPI
import dolfinx
import beat

def v_exact_func(x, t):
    return ufl.cos(2 * ufl.pi * x[0]) * ufl.cos(2 * ufl.pi * x[1]) * ufl.sin(t)

def s_exact_func(x, t):
    return -ufl.cos(2 * ufl.pi * x[0]) * ufl.cos(2 * ufl.pi * x[1]) * ufl.cos(t)

def ac_func(x, t):
    return (
        8
        * ufl.pi**2
        * ufl.cos(2 * ufl.pi * x[0])
        * ufl.cos(2 * ufl.pi * x[1])
        * ufl.sin(t)
    )

def simple_ode_forward_euler(states, t, dt, parameters):
    v, s = states
    values = np.zeros_like(states)
    values[0] = v - s * dt
    values[1] = s + v * dt
    return values

def main():
    M = 1.0
    T = 1.0
    t0 = 0.0

    comm = MPI.COMM_WORLD
    odespaces = ["P_1", "P_2", "DG_1"]
    Ns = [2**level for level in range(3, 8)]
    dts = [2 ** (-i) for i in range(3, 9)]
    fig, ax = plt.subplots(
        2,
        len(odespaces),
        figsize=(10, 8),
        sharey="row",
        sharex="row",
    )
    for k, odespace in enumerate(odespaces):
        errors = defaultdict(list)
        error_fname = Path(f"convergence_{odespace}.json")
        if not error_fname.is_file():
            for dt in dts:
                print(f"Running for dt={dt}")
                for N in Ns:
                    print(f"Running for N={N}")
                    mesh = dolfinx.mesh.create_unit_square(
                        comm,
                        N,
                        N,
                        dolfinx.cpp.mesh.CellType.triangle,
                    )
                    time = dolfinx.fem.Constant(mesh, dolfinx.default_scalar_type(0.0))
                    x = ufl.SpatialCoordinate(mesh)

                    t_var = ufl.variable(time)

                    s_exact = ufl.replace(s_exact_func(x, t_var), {t_var: T})
                    I_s = ac_func(x, t_var)

                    pde = beat.MonodomainModel(time=time, mesh=mesh, M=M, I_s=I_s)

                    V_ode = beat.utils.space_from_string(odespace, mesh, dim=1)
                    v_ode = dolfinx.fem.Function(V_ode)

                    s = dolfinx.fem.Function(V_ode)
                    s.interpolate(
                        dolfinx.fem.Expression(
                            s_exact,
                            V_ode.element.interpolation_points(),
                        ),
                    )

                    s_arr = s.x.array
                    init_states = np.zeros((2, s_arr.size))
                    init_states[1, :] = s_arr

                    ode = beat.odesolver.DolfinODESolver(
                        v_ode=v_ode,
                        v_pde=pde.state,
                        fun=simple_ode_forward_euler,
                        init_states=init_states,
                        parameters=None,
                        num_states=2,
                        v_index=0,
                    )
                    solver = beat.MonodomainSplittingSolver(pde=pde, ode=ode, theta=1.0)
                    solver.solve((t0, T), dt=dt)

                    v_exact = ufl.replace(v_exact_func(x, t_var), {t_var: T})

                    error = dolfinx.fem.form((pde.state - v_exact) ** 2 * ufl.dx)
                    E = np.sqrt(
                        comm.allreduce(dolfinx.fem.assemble_scalar(error), MPI.SUM),
                    )
                    errors[str(dt)].append(E)
            error_fname.write_text(json.dumps(errors))
        errors = json.loads(error_fname.read_text())
        errors_N = {}

        for i, N in enumerate(Ns):
            errors_N[N] = [errors[str(dt)][i] for dt in dts]
        lines_dt = []
        labels_dt = []
        for dt, errs in errors.items():
            (l,) = ax[0, k].loglog([1 / N for N in Ns], errs, "-o")
            lines_dt.append(l)
            labels_dt.append(f"dt={dt}")
        (l,) = ax[0, k].loglog(
            [1 / N for N in Ns],
            [5 / N**2 for N in Ns],
            "--",
            color="gray",
        )
        lines_dt.append(l)
        labels_dt.append("$O(h^2)$")
        (l,) = ax[0, k].loglog(
            [1 / N for N in Ns],
            [0.5 / N for N in Ns],
            ":",
            color="gray",
        )
        lines_dt.append(l)
        labels_dt.append("$O(h)$")

        ax[0, k].set_xlabel("N")
        lines_N = []
        labels_N = []
        for N, errs in errors_N.items():
            (l,) = ax[1, k].loglog(dts, errs, "-o")
            lines_N.append(l)
            labels_N.append(f"N={N}")
        (l,) = ax[1, k].loglog(
            dts,
            [dt**2 for dt in dts],
            "--",
            color="gray",
        )
        lines_N.append(l)
        labels_N.append(r"$O(\Delta t^2)$")
        (l,) = ax[1, k].loglog(
            dts,
            [0.08 * dt for dt in dts],
            ":",
            color="gray",
        )
        lines_N.append(l)
        labels_N.append(r"$O(\Delta t)$")

        ax[1, k].set_xlabel("dt")
        ax[0, k].set_title(" ".join(odespace.split("_")))
        if k == 0:
            ax[0, k].set_ylabel("Error vs N")
            ax[1, k].set_ylabel("Error vs dt")

    for axi in ax.flatten():
        axi.grid()
        axi.set_ylim([1e-3, 0.1])

    fig.subplots_adjust(right=0.8)
    fig.legend(
        lines_dt,
        labels_dt,
        loc="upper center",
        bbox_to_anchor=(0.9, 0.85),
    )
    fig.legend(
        lines_N,
        labels_N,
        loc="upper center",
        bbox_to_anchor=(0.87, 0.4),
    )

    fig.savefig("convergence.png")
    # rates = [np.log(e1 / e2) / np.log(2) for e1, e2 in zip(errors[:-1], errors[1:])]
    # cvg_rate = sum(rates) / len(rates)
    # print(rates)
    # breakpoint()
    # assert np.isclose(cvg_rate, 2, rtol=0.15)

if __name__ == "__main__":
    main()

Running for dt=0.125
Running for N=8

Running for N=16
Running for N=32
Running for N=64
Running for N=128

Running for dt=0.0625
Running for N=8
Running for N=16
Running for N=32
Running for N=64
Running for N=128

Running for dt=0.03125
Running for N=8
Running for N=16
Running for N=32
Running for N=64

Running for N=128

Running for dt=0.015625
Running for N=8
Running for N=16
Running for N=32
Running for N=64

Running for N=128

Running for dt=0.0078125
Running for N=8
Running for N=16
Running for N=32

Running for N=64

Running for N=128

Running for dt=0.00390625
Running for N=8
Running for N=16
Running for N=32

Running for N=64

Running for N=128

Running for dt=0.125
Running for N=8

Running for N=16
Running for N=32
Running for N=64

Running for N=128

Running for dt=0.0625
Running for N=8
Running for N=16
Running for N=32
Running for N=64

Running for N=128

Running for dt=0.03125
Running for N=8
Running for N=16
Running for N=32

Running for N=64

Running for N=128

Running for dt=0.015625
Running for N=8
Running for N=16

Running for N=32

Running for N=64

Running for N=128

Running for dt=0.0078125
Running for N=8

Running for N=16

Running for N=32

Running for N=64

Running for N=128

Running for dt=0.00390625
Running for N=8

Running for N=16

Running for N=32

Running for N=64

Running for N=128

Running for dt=0.125
Running for N=8

Running for N=16
Running for N=32
Running for N=64
Running for N=128

Running for dt=0.0625
Running for N=8
Running for N=16
Running for N=32
Running for N=64

Running for N=128

Running for dt=0.03125
Running for N=8
Running for N=16
Running for N=32

Running for N=64

Running for N=128

Running for dt=0.015625
Running for N=8
Running for N=16

Running for N=32

Running for N=64

Running for N=128

Running for dt=0.0078125
Running for N=8

Running for N=16

Running for N=32

Running for N=64

Running for N=128

Running for dt=0.00390625
Running for N=8

Running for N=16

Running for N=32

Running for N=64

Running for N=128